Somme de série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
par mathelot » 06 Sep 2010, 16:24
ore29360 a écrit:c'est ce que j'ai sur mon brouillon arnaud^^ c'etait juste pour simplifier. je vais essayer comme cela mathelot mais je ne suis pas trop
Dsl, ce que tu ne sembles pas avoir tout à fait compris, c'est comment on inverse une fonction bijective
a=tan(u) equivaut à u=arctan(a)
c'est une histoire d'appartenance au domaine de définition et d'appartenance au codomaine; un peu comme avec log et exponentielle
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
par ore29360 » 06 Sep 2010, 16:34
ah sisi sa je le biens tkt pas. ton a=tan(u) et ton b=tan(v) donc on a la meme chose. c'est juste que je ne peux factoriser le polynome....
-
mathelot
par mathelot » 06 Sep 2010, 16:40
Bon, c plus compliqué que prévu...
les numérateur et dénominateur d'une fraction sont définis
à un facteur k près.
Ex
=2kn)
=1-k(n^4+n^2+2))
a,b solutions de
)
le
' vaut
)
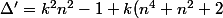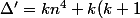 n^2+2k -1)
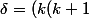)^2-4k(2k-1)=0)
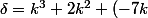 +4=0)
pour k=1 le
et le
est un carré parfait
-
mathelot
par mathelot » 06 Sep 2010, 16:43
mathelot a écrit:le
' vaut
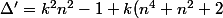bah si , c bon, tu m'as fait peur .pour le facteur trivial k=1
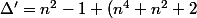=n^4+2n^2+1=(n^2+1)^2)
donc on trouve que a et -b sont bien des polynomes
de l'entier n..
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 06 Sep 2010, 16:48
Je poursuis avec l'idée du polynôme : on doit avoir que
 -P(n+1)}{P(n)P(n+1)+1} =\fr{2n}{n^4+n^2+2})
ce qui entraîne que
-P(n+1\)(n^4+n^2+2) =2n\(P(n)P(n+1)+1\))
. Si on note
le degré de P, on a, puisque le degré de
-P(X+1))
est
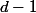
que
donc
soit
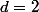
. Il ne reste "plus qu'à" trouver les coefficients de
.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 07 Sep 2010, 17:51
Essayons d'y voir clair ...
soit
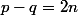
et
et-
sont racines de
ce qui donne (facilement)
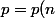=n^2-n+1)
et
=n^2+n+1=p(n+1))
à toi de conclure...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
