Somme de série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 14:56
par ore29360 » 06 Sep 2010, 14:56
bonjour j'ai un problème avec deux sommes de série:
arctan(2n/n^4+n²+2) et 1/n!.
pour la seconde j'ai fait avec taylor lagrange sa me paraissait bien mais mon resultat est faux, peut etre une erreur de ma part.
et pour la première j'ai utilisé la méthode télescopique mais sa ne me donne rien. pourriez vous m'indiquez une bonne voie de recherche. merci d'avance
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 06 Sep 2010, 15:11
par MacManus » 06 Sep 2010, 15:11
Bonjour.
Tu sais sans doute que la fonction exponentielle admet le développement en série suivant :
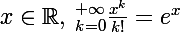
. Tu peux en déduire la somme de la série
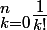
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:23
par ore29360 » 06 Sep 2010, 15:23
ba je trouve e en reponse avec mon truc ce qui correspond au tien mais si on fait avec les quelques 3 ou 4 premiers termes on depasse deja la valeur de e
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 06 Sep 2010, 15:29
par Arnaud-29-31 » 06 Sep 2010, 15:29
ore29360 a écrit:mais si on fait avec les quelques 3 ou 4 premiers termes on depasse deja la valeur de e
?? Non la réponse est bien e.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 06 Sep 2010, 15:35
par MacManus » 06 Sep 2010, 15:35
ore29360 a écrit: si on fait avec les quelques 3 ou 4 premiers termes on depasse deja la valeur de e
Ah bon ? combien fait la somme des 3 premiers termes par exemple ?
(e = 2,718....)
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:37
par ore29360 » 06 Sep 2010, 15:37
bon ba je sais pas^^ pour sa fesait 1 + 1 + 1/2 deja car 0!=1...
fin si c'est la bonne reponse c'est bon alors. et pour l'autre vous n'avez pas d'idée??
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 06 Sep 2010, 15:41
par MacManus » 06 Sep 2010, 15:41
oui et 1+1+(1/2) = 5/2 = 2,5. A priori pas de problèmes
-
mathelot
 par mathelot » 06 Sep 2010, 15:41
par mathelot » 06 Sep 2010, 15:41
Bj,
pour la (1), il faut essayer la téléscopie
qui dit téléscopie , dit soustraction
partons de
=\frac{tan(u)-tan(v)}{1+tan(u)tan(v)})
poses
a=tan(u) et b=tan(v), ce qui permet d'inverser la relation
une fois que tu auras fait ça,
tu pourras identifier
a+(-b)
et
1+ab
d'où finalement un trinome du second degré avec somme et produit des racines..
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 15:42
par girdav » 06 Sep 2010, 15:42
Pour la première, on pourrait procéder de manière analogue au calcul de la somme de la série de terme général
)
. On a
=\fr{\fr 1n -\fr 1{n+1}}{1+\fr 1{n(n+1)}}=<br />\fr{1}{n^2+n+1})
et on a bien fait apparaître une série télescopique.
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:43
par ore29360 » 06 Sep 2010, 15:43
ba j'ai essayé cela mais mon trinome n'a pas de solution sur R... je trouve cela bizard .
-
mathelot
 par mathelot » 06 Sep 2010, 15:44
par mathelot » 06 Sep 2010, 15:44
ore29360 a écrit:pourriez vous m'indiquez une bonne voie de recherche
Il demandait une piste..
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 15:48
par girdav » 06 Sep 2010, 15:48
Pour appliquer ce qui je viens de faire, il suffit de trouver un polynôme

tel que le terme général de la série en question s'écrive
}-\arctan \fr 1{P(n)})
.
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:57
par ore29360 » 06 Sep 2010, 15:57
j'arrive à:
2n=tan(u)-tan(v)
n^4+n²+2=1+tan(u)tan(v)
et la je bloque...
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:58
par ore29360 » 06 Sep 2010, 15:58
en general on fait sa quand il y a un produit au denominateur non??
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 15:59
par ore29360 » 06 Sep 2010, 15:59
et girdav je suis d'accord c'est ce que jessaie de faire sauf que je ne trouve pas ce qu'il faut mettre....
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 16:11
par girdav » 06 Sep 2010, 16:11
Pour trouver le polynôme

, tu peux écrire que
}-\arctan \fr 1{P(n)}\) =\fr{2n}{n^2+n+1})
puis utiliser la formule de
)
.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 06 Sep 2010, 16:12
par Arnaud-29-31 » 06 Sep 2010, 16:12
ore29360 a écrit:j'arrive à:
2n=tan(u)-tan(v)
n^4+n²+2=1+tan(u)tan(v)
et la je bloque...
Oui c'est bien ça ... seulement la notation u et v me gène un peu : ils sont liées ce sont deux termes consécutif d'une même suite.
J'aurais écris
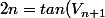 - tan(V_n))
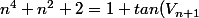.tan(V_n))
Avec

une suite telle que
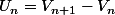
-
mathelot
 par mathelot » 06 Sep 2010, 16:17
par mathelot » 06 Sep 2010, 16:17
re,
=\frac{tan(u)-\tan(v)}{1+ tan(u) tan(v)})
posons a=tan(u) b= tan(v)
d'où
u=arctan(a) b =arctan(v)
=\frac{a-b}{1+ ab})
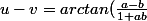)
=arctan(a)-arctan(b))
Il suffit de résoudre le système d'inconnues (a,b)
=2n)
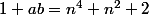
d'où somme et produit des racines
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 16:21
par ore29360 » 06 Sep 2010, 16:21
c'est ce que j'ai sur mon brouillon arnaud^^ c'etait juste pour simplifier. je vais essayer comme cela mathelot mais je ne suis pas trop
-
ore29360
- Membre Naturel
- Messages: 56
- Enregistré le: 13 Sep 2007, 21:50
-
 par ore29360 » 06 Sep 2010, 16:22
par ore29360 » 06 Sep 2010, 16:22
non en fete c'est exactement ce que j'ai relis au dessus. mais arriver la le polynome ne se factorise pas sur R d'ou mon probleme. ou alors j'ai un énorme trou sur des math basiques^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
