Croissance d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 14:22
par Kiwii » 04 Sep 2010, 14:22
Voilà, j'essaie pas mal de choses mais je m'embrouille, j'arrive à rien..
Auriez vous une suggestion pour montrer que la suite:
u(n):=
}n(n-1)^{n-1}}{(2n-1)^{n-1/2}\int_0^1\!x^n(1-x)^n\,dx})
est croissante?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 04 Sep 2010, 14:32
par fatal_error » 04 Sep 2010, 14:32
salut,
jpense qu'on peut calculer le rapport
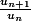
et le comparer par rapport à 1
la vie est une fête

-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 17:48
par Kiwii » 04 Sep 2010, 17:48
Deja essayé.. mais c'est pas simple
-
mathelot
 par mathelot » 04 Sep 2010, 18:18
par mathelot » 04 Sep 2010, 18:18
Bj
effectivement il suffit de former le quotient
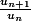
après tout ce qui est de la forme
^n)
tend vers exp(y)
tu vas voir; ça se simplifie bien,
dans les
exposants de forme affine n+3, il faut isoler le cube
en un facteur séparé pour travailler sur l'exposant
n tout seul
pour la
base de forme 2n-1, factoriser le 2
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 19:06
par Kiwii » 04 Sep 2010, 19:06
aoups j'avais oublié un truc, j'ai mal recopié..
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 19:50
par Kiwii » 04 Sep 2010, 19:50
puis j'ai du mal à comprendre le fait que si qqchose est equivalent à autre chose en l'infini ils aient même variation
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Sep 2010, 19:54
par girdav » 04 Sep 2010, 19:54
Que penses-tu de

et

?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Sep 2010, 19:57
par girdav » 04 Sep 2010, 19:57
As-tu calculé l'intégrale?
Par ailleurs, je suis curieux de savoir d'où vient l'exercice?
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 20:04
par Kiwii » 04 Sep 2010, 20:04
je ne sais pas d'où sort l'exercice..
non je n'ai pas calculé l'integrale
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 04 Sep 2010, 20:40
par Kiwii » 04 Sep 2010, 20:40
Qu'est ce que tu veux me faire dire sur 1+1/n et 1-1/n?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 05 Sep 2010, 08:52
par girdav » 05 Sep 2010, 08:52
Kiwii a écrit:Qu'est ce que tu veux me faire dire sur 1+1/n et 1-1/n?
C'est pour voir que deux suites équivalentes en

n'ont pas nécessairement le même sens de variation.
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 05 Sep 2010, 16:28
par Kiwii » 05 Sep 2010, 16:28
oui c'est bien comme ça que je pensais.. Donc ca ne me sert à rien non plus pour le sens d'orientation d'etudier la limite de
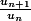
...
En ce cas je ne vois pas trop comment simplifier..
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 05 Sep 2010, 19:41
par Kiwii » 05 Sep 2010, 19:41
Pour ce qui est de l'integrale, je trouve :
^{k}}{n+k+1})
que je n'arrive pas à simplifier..
Donc ca n'aide pas trop non plus..
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 06 Sep 2010, 16:47
par Kiwii » 06 Sep 2010, 16:47
aucune idée?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 16:55
par girdav » 06 Sep 2010, 16:55
Je vais essayer de voir si on peut calculer l'intégrale autrement, par exemple en posant
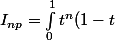^p dt)
.
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 06 Sep 2010, 20:00
par Kiwii » 06 Sep 2010, 20:00
d'accord, merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 20:43
par girdav » 06 Sep 2010, 20:43
Bon, un truc sympa est que l'on a
^{y-1}dt =\fr{\Gamma (x)\Gamma(y)}{\Gamma(x+y)})
où

est définie pour tout

par
= \int_0^{\infty}t^{x-1}e^{-t}dt)
.
Le truc "génial" est que pour tout entier

on a
)
a à voir avec

donc ça simplifie le rapport.
-
romi64
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Sep 2010, 13:50
-
 par romi64 » 06 Sep 2010, 20:58
par romi64 » 06 Sep 2010, 20:58
Bonsoir
A vue de nez l'intégrale me fait penser à la fonction béta ! :zen: Si tu veux calculer cette intégrale tu peux intégrer par parties et faire une récurrence sur n
-
Kiwii
- Membre Naturel
- Messages: 29
- Enregistré le: 25 Déc 2008, 19:44
-
 par Kiwii » 06 Sep 2010, 21:09
par Kiwii » 06 Sep 2010, 21:09
Oh oui! merci beaucoup, ça me plait bien tout ça!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 21:26
par girdav » 06 Sep 2010, 21:26
Bon, sinon avec la méthode traditionnelle on a
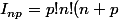!})
.
Après, on doit regarder si le quotient s'arrange bien, surtout vis-à-vis des autres termes qui constituent

:
!}\fr{(2n+2)!}{(n+1)!(n+1)!}\\<br />&= \fr{(2n+2)(2n+1)}{(n+1)^2}\\<br />&=2\fr{2n+1}{n+1}.<br />\end{align})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités