Réels, naturels, relatifs, rationnels...

[cami//e]

bonjour,
j'ai un problème qui porte sur les réels, naturels, relatifs, rationnels...
J'essaye de faire la difference entre tous, mais j'ai des trous...
Par exemple :
- quelle est la définition exacte des rationnels ?
J'ai trouvé "l'ensemble des des nombres admettant une ecriture decimale illimité périodique", j'ai compris la phrase.
Mais je trouve bizarre que sur un schéma de cours, les rationnels englobent les décimales (qui eux même englobent les relatifs qui englobent les naturels).
Alors que les rationnels sont plus précis que les décimales non ?
C'est pas dans l'autre sens ?

merci de me sortir de ce mic mac :marteau: ,

cami//e

[Arnaud-29-31]

Salut Camille,
Une première définition des rationnels avant de s'attarder sur celle que tu cites serait tout nombre qui peut s'écrire de la forme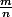 avec m et n des entiers. (n non nul bien sur ...)

Tu as tout d'abord l'ensemble N : les entiers naturels ( 0,1,2, ....)
Ensuite l'ensemble Z : les entiers relatifs (C'est l'ensemble N auquel on ajoute les nombres comme -1,-2,-3, ...)
Ensuite l'ensemble Q : les rationnels (C'est l'ensemble Z auquel on ajoute les nombres comme , ...)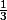
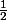Puis pour finir l'ensemble R : les réels (C'est l'ensemble Q auquel on ajoute les nombres comme , , ...)


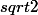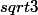Les nombre réels qui ne sont pas rationnels ont un développement décimal illimité : par exemple = 3,14159265359 ... et ca ne s'arrête jamais.

En revanche un nombre rationnel peut avoir un développement décimal limité : par exemple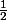 = 0.5 et c'est tout.
Ou bien il peut avoir un développement illimité : par exemple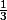 = 0.3333333333 ... et une infinité de 3, on remarque ici une écriture périodique : le 3 qui se répète.
Si on prend le rationnel = 1.09090909 ... c'est le '09' qui se répète ...
D'où la définition que tu as trouvé.


Enfin, pour répondre à ta 2eme question, si l'on ajoute l'ensemble des nombres décimaux, il est bien englobé par Q.
En effet, un nombre décimal est un nombre qui admet un développement décimal limité et comme je viens de le dire un nombre appartenant à Q peut avoir un développement décimal limité ou illimité.

1/2 et 1/3 sont tout deux rationnels, cependant 1/2 est un nombre décimal, 1/3 ne l'est pas ...

[cami//e]

merci Arnaud-29-31, tu me sauve ! :id:
J'ai tout compris (chose rare) et en plus je peux tout réécrire sur une fiche rappel vu que c'est simple et pertinent !
merci beaucoup ! :we:

[Arnaud-29-31]

De rien, de rien :)
Tu me fais rougir là :oo

[oscar]

shéma


http://yfrog.com/0tensembledesnom

[Dinozzo13]

Salut !

Je tiens un peu à expliciter la définition sur les nombres décimaux :
Ce sont tous les nombres de la forme : où appartient à et et appartiennent à .
ex : est décimal car

[oscar]

shéma



http://yfrog.com/bfensembledesnombresj