Suite de fibonnaci

[louis1°S]

et aussi
comment demontrez vous le fait que dans la suite de fibonnaci...

la suite est telle que: Fn(n+2) = Fn(n+1) + Fn F0=0 F1=1

comment montrer que PGCD(Fn(n+1) , Fn(n) ) = 1
autrement dit que deux termes consecutifs de la suite sont premiers ?

[girdav]

La formule de récurrence ne te permet-elle pas d'écrire l'algorithme d'Euclide?
PS : deux termes consécutifs sont premiers entre eux et non premiers. De plus, on note et non le n-ième terme de cette suite.

[louis1°S]

oui mais jai pas lancer word...
comment fait on avec l'algorithme d'euclide ?

[benekire2]

Salut, simplement par l'absurde et par récurrence. Si p divise F(n+1) et F(n+2)=F(n+1)+F(n) alors p divise F(n) par différence. C'est absurde.

[girdav]

Sinon je crois que l'on peut y aller plus simplement. Si d divise à la fois et alors d divise aussi .

[louis1°S]

Salut, simplement par l'absurde et par récurrence. Si p divise F(n+1) et F(n+2)=F(n+1)+F(n) alors p divise F(n) par différence. C'est absurde.

je ne comprends pas le raisonnement

Par définition Fn(n+2) = Fn(n+1) + Fn(n)
Si d divise Fn(n+1)
Pourquoi sachant que Fn(n+1) = Fn(n+2) + Fn(n)
Alors d divise Fn ??

[benekire2]

Déjà tu t'acharnes avec tes notations ...

La suite de fibo c'est et puis pour n>1

Donc tu montre la proproété jusqu'au rang n+1 et alors au rang n+2 pour l'hérédité tu as :

donc tu suppose que p divise à la fois et et il faut se rappeler que si p|a et p|b alors pour tout entiers u et v p|(ua+uv) ainsi comme ici p divise et alors p divise et donc cela vient contredire l'hypothèse de récurrence.

[girdav]

Pour le coup pas besoin de raisonner par l'absurde : il suffit de montrer que le seul diviseur commun (positif) à et est 1.
On peut faire une récurrence rapide pour montrer que F_{n-k} est divisible par pour 1 si et le sont.

[louis1°S]

[mathelot]

Bj,

je ne l'ai pas fait mais je sais qu'il est fabuleux ...

on appelle (F) la suite de Fibonacci.
on appelle le nombre d'or
avec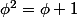

1) montrer que pour tout ,

2)a)On suppose que l'algorithme d'Euclide appliqué à a et b
demande n opérations. (on a donc et

en notant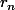 les restes des étapes successives de l'algorithme.
Montrer que et

passage obscur

b)Montrer que l'algorithme d'Euclide appliqué à et
demande n itérations.

c)Déduire de ce qui précède que le nombre n d'itérations
de l'algorithme d'Euclide pour a et b vérifie

et

d) en déduire que n=5p où p est le nombre de chiffres de b
(on suppose a=b)
e) quelle est la complexité de l'algorithme d'Euclide?

il faut tester cet exo et le mettre au point mais l'idée est là:
la suite de Fibonacci donne un majorant de la longueur de l'algorithme d'Euclide :id:

@+

[mathelot]

finalement, c'est un résultat très connu: l'algorithme d'Euclide et le théorème de Lamé