Récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 16:11
par Sky29 » 01 Sep 2010, 16:11
Voila bien un thème ou j'éprouve le plus de difficultées,
Montrer par réccurence que :
Somme (k=1 à k=n) de k(k!) = 1(1!)+2(2!)+...+n(n!)=(n+1)!-1
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 16:18
par MacManus » 01 Sep 2010, 16:18
Bonjour
Eh bien quelles sont les étapes d'une démonstration par récurrence ?
(la récurrence se fait sur l'entier n > 0)
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 16:25
par Sky29 » 01 Sep 2010, 16:25
1) Initialisation : On montre que la formule est valable au rang 1, ce qui est le cas
2) Démonstration de la formule au rang n+1
Mais c'est la que j'ai un soucis.
3) Conclusion
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 16:31
par Sky29 » 01 Sep 2010, 16:31
Sn = (n+1)!-1
Sn+1 = (n+2)!-1 ?
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 16:32
par MacManus » 01 Sep 2010, 16:32
Ok pour l'initialisation.
on suppose la formule vérifiée au rang n > 0.
Au rang n+1, on écrit :
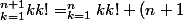(n+1)!)
ok ? essaye de continuer !
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 16:33
par MacManus » 01 Sep 2010, 16:33
Sky29 a écrit:Sn = (n+1)!-1
Sn+1 = (n+2)!-1 ?
oui c'est ce résultat que tu dois montrer. C'est bien d'écrire hypothèse et résultat sous les yeux!
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 16:33
par Sky29 » 01 Sep 2010, 16:33
Merci en tout cas, je vai voir ca.
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 16:57
par Sky29 » 01 Sep 2010, 16:57
J'ai divisé cette somme en deux sommes, l'une avec k(k!) et l'autre avec (n+1)(n+1)!
Dites moi si c'est le bon chemin, parceque après ca j'ai ésaille d'autres calculs cela ne me mène à rien...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 17:02
par MacManus » 01 Sep 2010, 17:02
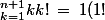+2(2!)+...+n(n!) \:+(n+1)(n+1)! \: = \: \bigsum_{k=1}^{n}kk!\: +(n+1)(n+1)! \: = \: (n+1)!-1 \: + (n+1)(n+1)!)
(je ne sais pas si tu as vu le post #5)...
La dernière égalité est justifiée en utilisant l'hypothése de récurrence (au rang n).

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 01 Sep 2010, 17:04
par fatal_error » 01 Sep 2010, 17:04
salut,
j'avais vu une astuce je crois que c'est nuage mais je sais plus.
Ca consistait à ecrire
kk! = (k+1-1)k! = (k+1)! - k!
la vie est une fête

-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 17:08
par Sky29 » 01 Sep 2010, 17:08
J'ai vu le post 5, je suis arrivé à la même chose que vous, à savoir,
(n+1)!-1+(n+1)(n+1)!, à la suite de ca, j'ai factorisé par (n+1)! pour obtenir,
(n+1)!(n+2)-1
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 17:10
par MacManus » 01 Sep 2010, 17:10
à Fatal_error
ouais ça roule tout aussi bien!
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Sep 2010, 17:11
par MacManus » 01 Sep 2010, 17:11
Sky29 a écrit:J'ai vu le post 5, je suis arrivé à la même chose que vous, à savoir,
(n+1)!-1+(n+1)(n+1)!, à la suite de ca, j'ai factorisé par (n+1)! pour obtenir,
(n+1)!(n+2)-1
Ok eh bien c'est fini !
et oui : (n+2)(n+1)! = (n+2)!
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 17:17
par Sky29 » 01 Sep 2010, 17:17
Le soucis est que mon prof de Terminale ne c'est pas attardé sur ce genre de calcul, pourriez vous m'expliquer pourquoi : (n+2)(n+1)! = (n+2)!
Parceque là je nage dans le flou total
-
AL-kashi23
- Membre Rationnel
- Messages: 765
- Enregistré le: 14 Aoû 2007, 10:59
-
 par AL-kashi23 » 01 Sep 2010, 17:37
par AL-kashi23 » 01 Sep 2010, 17:37
Sky29 a écrit:Le soucis est que mon prof de Terminale ne c'est pas attardé sur ce genre de calcul, pourriez vous m'expliquer pourquoi : (n+2)(n+1)! = (n+2)!
Parceque là je nage dans le flou total
Par définition ? (n+2)!=(n+2)*(n+1)*n*(n-1).....*3*2*1=(n+2)*(n+1)!
-
Sky29
- Membre Naturel
- Messages: 34
- Enregistré le: 18 Avr 2007, 12:53
-
 par Sky29 » 01 Sep 2010, 18:36
par Sky29 » 01 Sep 2010, 18:36
Merci à tous ceux qui m'ont donné des explications.
Cependant, je ne réussi pas à comprendre le principe que tu m'as montré Al-kashi23, aurais tu un site à me proposer ou je puisse revoir tout cela stp.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
