Suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 30 Aoû 2010, 15:54
par skater41 » 30 Aoû 2010, 15:54
Donc, si je ne me trompe pas:
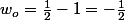
donc
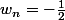
x
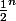
Est-ce bien ça ?
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Aoû 2010, 16:01
par Djmaxgamer » 30 Aoû 2010, 16:01
oui, sauf la notation
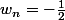
x
^n)
(sinon ca fait
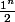
) mais on va mettre ca sous le compte de la notation LATEX :we: .
A partir de la, quelle est l'expression de

en fonction de n ?
Puis celle de

?
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 30 Aoû 2010, 16:16
par skater41 » 30 Aoû 2010, 16:16
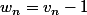
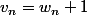
=-

x
^n+1)
Je ne suis pas sûr pour le signe du 1.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Aoû 2010, 16:18
par Djmaxgamer » 30 Aoû 2010, 16:18
C'est correct.
Donc

= ?
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 30 Aoû 2010, 16:22
par skater41 » 30 Aoû 2010, 16:22
Tout simplement
^n+1})
C'est un multiplié entre les deux, j'arrivais pas à mettre un x
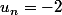
x
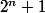
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Aoû 2010, 16:35
par Djmaxgamer » 30 Aoû 2010, 16:35
skater41 a écrit:Tout simplement
^n+1})
C'est un multiplié entre les deux, j'arrivais pas à mettre un x
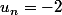
x
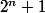
pour mettre un x la commande latex est \times
Pour ta première expression c'est bon mais pas la deuxième. En définitive, quelle est l'expression de

en fonction de n ?
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 30 Aoû 2010, 16:38
par skater41 » 30 Aoû 2010, 16:38
J'aurai dit les deux, vu que j'ai fait l'inverse des nombres au dénominateur pour avoir la deuxième expression
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Aoû 2010, 16:42
par Djmaxgamer » 30 Aoû 2010, 16:42
skater41 a écrit:J'aurai dit les deux, vu que j'ai fait l'inverse des nombres au dénominateur pour avoir la deuxième expression
c'est incorrect
^n+1}= \frac{1}{-\frac{1}{2^{n+1}}+1} = \frac{1}{\frac{2^{n+1}-1}{2^{n+1}}} = \frac{2^{n+1}}{2^{n+1}-1})
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 30 Aoû 2010, 16:51
par skater41 » 30 Aoû 2010, 16:51
Merci beaucoup ! :we:
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Aoû 2010, 16:52
par Djmaxgamer » 30 Aoû 2010, 16:52
Question : la suite converge-t-elle ? Si oui, vers quelle valeur ?
Tu pourra utiliser l'expression de

en fonction de n qu'on vient de déterminer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités