Execice produit scalaire

[laetitia1322]

bonjours à tous

ABCD est un carré de coté a ; I et J sont les milieux respectifs de [AB] et [BC] : les droites (AJ) et (IC) se coupent en K
On note O l'angle géométrique JKC

1. caculer les produit scalaire vecAJ.vecIB et vec AJ.vec BC

en déduire vecAJ.vecIC

2 calculer la valeur exacte des longueurs AJ et IC

3 déterminer la valeur exacte de cos O .

alors pour la premiere je pense

vecAJ.vecIB = AJ ² * (a/2)² * cos (O)
vecAJ .vecBC = AJ² * a² * cos (O)

après je ne sais plus je ne comprends pas je ne comprend rien au produit scalaire
merci d'avance

[mathelot]

Bj,


voici quelques explications sur le produit scalaire. Lis-les attentivement.

a)

Soit ABC un triangle rectangle en A.

La quantité


est nulle.

oui, car c'est (moitié de) la quantité de Pythagore :id:

b)
Si ABC n'est plus nécessairement un triangle rectangle mais quelconque:

on peut encore calculer


On remarque que

i) si l'angle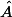 est aigü , alors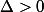
ii) si l'angle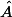 est obtus , alors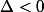
iii) que cette quantité vérifie les propriétés
d'un produit,car


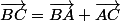
et qu'elle ressemble formellement à l'expression

<---produit

pour plus de détails, lire par exemple Terracher,Transmaths ou Hachette
de 1ère. Emprunte-les au CDI.

[mathelot]

re,

sur les cinq cours que tu trouve en ligne (google="cours produit scalaire")
un seul expose le produit scalaire à partir de la "quantité de Pythagore"



Cette exposition facilite grandement la compréhension car elle
reprend des notions vûes en 4ème.

La seule chose à comprendre, dès lors, est que cette quantité
est un "double produit"
ici

[laetitia1322]

ah je crois que j'ai compris :
je calcule AJ grace a pythagore
donc je trouve AJ= 3a/2 : cest ça ?

et donc vecAJ.vecIB = 1/2 [( 3a/2+a/2)² -(3a/2)² -(a/2)² ]
= 1/2 (16a²/4 - 10a²/4
= 1/2 ( 6a²/4)
= 6a²/4 * 1/2
= 3a²/4

c'est ça ?

[mathelot]

Salut,

malheuresement, il y a beaucoup de travail à fournir pour maitriser
le produit scalaire

1) lire un cours utilisant la quantité de Pythagore

2) une fois que le cours est (à peu près compris), utiliser les 5 formules
au choix. Selon les cas, certaines marchent mieux que d'autres









où A' et B' sont les projetés orthogonaux de C et D sur (AB)




Toutes les expressions avec des carrés sont des carrés de distances
et peuvent être calculées avec Pythagore

[mathelot]

ah je crois que j'ai compris :
je calcule AJ grace a pythagore
donc je trouve AJ= 3a/2 : cest ça ?

et donc vecAJ.vecIB = 1/2 [( 3a/2+a/2)² -(3a/2)² -(a/2)² ]
= 1/2 (16a²/4 - 10a²/4
= 1/2 ( 6a²/4)
= 6a²/4 * 1/2
= 3a²/4

c'est ça ?

oui, extra :++: juste une petite erreur : en calculant

dans la formule que tu utilises, ça demande de calculer


le souçi, c'est que le calcul de cette somme est loin d'^tre immédiat.

sinon, tu peux utiliser les projetés orthogonaux de A et J
sur (AB) qui sont respectivement A et B.

[laetitia1322]

je ne comprends toujours pas alors mon calcul est faux et AJ ² je ne comprends pas non plus pk ce résultat

[laetitia1322]

s'il vous plait aidez moi ... :triste:

[mathelot]

ah
je calcule AJ grace a pythagore
donc je trouve AJ= 3a/2 : cest ça ?

et donc vecAJ.vecIB = 1/2 [( 3a/2+a/2)² -(3a/2)² -(a/2)² ]

ta formule , içi, ne fonctionne pas pour deux raisons:
- la somme est une somme vectorielle,
elle s'évalue en traçant la diagonale d'un parallèlogramme
malcommode. En effet, ce parallèlogramme est coincé entre
un sommet du rectangle et le milieu du petit côté

- même si le parallélogramme était "pratique", ta formule de Pythagore
ne marcherait qu'avec un rectangle

solution
i) soit, tu utilise la double distributivité du produit scalaire
relativement à l'addition des vecteurs en prenant comme repère
deux vecteurs orthogonaux sur le bord du rectangle

ou plus simplement

ii) on utilise la formule du "projeté orthogonal"
ie, pour calculer
on peut remplacer un des vecteurs par son projeté
sur l'autre direction de droite (AB)

[mathelot]

Salut,

ce n'est pas pour être lourd (enfin si :we: ) mais as tu la méthodologie ?

il faut que tu étudies les choses dans l'ordre sinon ça risque d'être difficile

AVANT le produit scalaire:

est-ce que la somme de 2 vecteurs est bien connue ?

?

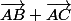a) avec la règle du parallélogramme ?
b) avec les points à la queue leu-leu ? (Chasles: A-->B--->C)

ce n'est pas la peine de faire du produit scalaire si tu ne sais pas
additionner deux vecteurs: c'est mettre la charrue avant les boeufs :hum:

[laetitia1322]

j'ai bien compris le projeter cependant dans tous les cas que vous m'avez donné les vecteurs se croisent .... Aj et IB n'ont aucun point en commun j'ai la figure qui était données dans l'énoncé puis j ai appris à faire le projeté qu'avec trois points dans un triangle la dans le cas de mon énoncé I est le milieu de AB et AJ et IB ne forment pas un triangle c'est AJB le triangle rectangle

[mathelot]

j'ai bien compris le projeter cependant dans tous les cas que vous m'avez donné les vecteurs se croisent

Ce n'est pas ta faute mais tu as une conception erronée des vecteurs..

deux vecteurs et
sont les mêmes si les segments [BC] et [AD] ont même milieu

Cette définition conduit à la notion de "vecteur libre"
On prend l'origine du vecteur où l'on veut.
Donc les vecteurs "ne se croisent pas".

Aj et IB n'ont aucun point en commun

On peut remplacer par . ce sont les mêmes
vecteurs (libres)

j ai appris à faire le projeté

remplace par :
C'est çà "projeter A et J sur la droite (AB)"

[laetitia1322]

donc je fais IB = AI donc comme B est le projeté de J alors
AJ.IB = AB.IB
= a * a/2
= a² /2
cest ça ?

mais pour la dexieme je ne comprends pas

[laetitia1322]

s'il vous plait , sa fait 4 jours que je réfléchis dessus mais j'ai du mal ....