Produit scalaire

[laetitia1322]

bonjour à tous ,

ABCD est un rectangle tel que AB=4 et BC= 3 . ABF est un triangle équilatéral , BCE est un triangle rectangle et isocèle en C
ABF et BCE sont à l'extérieurs à ABCD

1 . calculer les produits scalaires DC.AF , EB.DC ET CE.DA
2. calculer les produits scalaires CB.DF et DB.AC en utilisant la relation de chasles et la linéarité du produit scalaire

La 1 / jai trouvé DC.AC = 16
EB.DC=12racine2
CE.DA=9

Pour la 2 je n'est rien compris je cherche mais sans réponse

Merci d'avance de votre aide (PS: jai de grosses diffilcultés pour le produit scalaire

[Djmaxgamer]

Je ne sais pas si ton problème réside uniquement dans la compréhension de la question, mais dans un premier temps, voyons ce que signifient les termes de la question.

"relation de chasles" tu dois la connaître :

"linéarité du produit scalaire" (où plutôt sa bilinéarité) signifie que :

En utilisant ces relations, tu peux transformer ses produits scalaires en somme de produits scalaires calculés précédemment (je les ai pas vérifiés)

[laetitia1322]

je voudrai savoir si mes calculs précédents étaient juste :hein:

[laetitia1322]

bonjours à tous

ABCD est un carré de coté a ; I et J sont les milieux respectifs de [AB] et [BC] : les droites (AJ) et (IC) se coupent en K
On note O l'angle géométrique JKC

1. caculer les produit scalaire vecAJ.vecIB et vec AJ.vec BC

en déduire vecAJ.vecIC

2 calculer la valeur exacte des longueurs AJ et IC

3 déterminer la valeur exacte de cos O .

alors pour la premiere je pense

vecAJ.vecIB = AJ ² * (a/2)² * cos (O)
vecAJ .vecBC = AJ² * a² * cos (O)

après je ne sais plus je ne comprends pas je ne comprend rien au produit scalaire
merci d'avance de votre aide

[Dinozzo13]

Salut !
Perso moi je trouve :
or toi tu calcules



Mais n'ayant pas triaté de produit scalaire depuis un moment je doute.

[laetitia1322]

et comment avez vous fait pour trouver ses résultats vous avez utiliser la formule avec le cosinus ?

[Dinozzo13]

en utilisant la definition ca devrait le faire

[geegee]

Bonjour,

CB.DF=CB.(DA+AF)=CB.DA+CB.AF=9+3.4.cos(4/3 PI)=3

[ppcrepin]

Bonjour :

DC.AF = ||DC||*||AF||*cos(Pi/3)= 4*4*1/2 = 8

EB.DC = ||EB||*||DC||*cos(3Pi/4) = 3sqrt(2)*4*(-sqrt(2)/2) = - 12

quant au dernier produit scalaire il est nul car il y a perpendicularité

[Dinozzo13]

Ca confirme donc que je n'ai pas oublié les porduit scalaire ^^

Je vais te rédiger le premier pour te montrer un exemple :

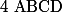est un rectangle donc .
Soit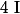 le milieu de .
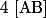est un triangle équilatéral donc 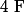se projette orthogonalement en 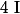sur 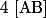et par conséquent :

Or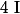 est le milieu de 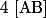donc , on a donc :


ou


Or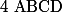 est un recrangle donc et est équilatéral donc
De plus :
car 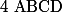étant un rectangle, on a :
Comme dit précédement, étant équilatéral :

Par conséquent :


@+ :++:

[laetitia1322]

merci pour vos réponses cela a beaucoup aider ppour la question 1 pour la question 2 j'ai compris cependant moi mon calcul cest
CB.DF= CB.DA+ CB.AF = 9+3*4*cos (pi/3 ) = 15
est-ce la meme chose que le calcul de gege ?

De plus pour BD.AC = (DA+AB) ( AB+BC)
= DA.AB + DA.BC + AB.AB+ AB.BC
= 0 + 3*3*cos 0 + 4 * 4 *cos 0 + 0
= 9 + 16
= 25

est ce cela ?