Bonjour,
Intégrale tirée de l'équation de la chaleur en thermoplasticité :
integrale : dT / [1-(a.T+b)^m]
J'ai regardé sur sosmaths mais j'ai rien trouvé de comparable et Maple n'est pas à même de calculer cette intégrale.
Quelqu'un aurait-il une idée ?
Merci d'avance.
Intégration dT/(1-u(T)^m)
6 messages
- Page 1 sur 1
Salut,
Au départ je cherchais une primitive mais maintenant comme toi j'ai des doutes sur la faisabilité.
En fait j'ai une équation de la forme :
k.dT/(1-(a.T+b)^m)=(c+d.W^n).dW
avec k, a, b, c, d, n, m des constantes et T et W les variables. J'aurai souhaité avoir l'évolution de T en fonction de W.
T est intégrée de T0 à T et W de 0 à W.
Au départ je cherchais une primitive mais maintenant comme toi j'ai des doutes sur la faisabilité.
En fait j'ai une équation de la forme :
k.dT/(1-(a.T+b)^m)=(c+d.W^n).dW
avec k, a, b, c, d, n, m des constantes et T et W les variables. J'aurai souhaité avoir l'évolution de T en fonction de W.
T est intégrée de T0 à T et W de 0 à W.
Si je comprends bien, tu cherches à intégrer  . Or tu peux factoriser ce polynôme dans C et t'en servir pour faire une décomposition en éléments simples. Ensuite, je pense qu'en regroupant ces éléments 2 à 2 de façon judicieuse, tu vas pouvoir intégrer. Mais bon, ça ne te donnera qu'une somme de Arctan, ce qui n'est pas franchement pratique...
. Or tu peux factoriser ce polynôme dans C et t'en servir pour faire une décomposition en éléments simples. Ensuite, je pense qu'en regroupant ces éléments 2 à 2 de façon judicieuse, tu vas pouvoir intégrer. Mais bon, ça ne te donnera qu'une somme de Arctan, ce qui n'est pas franchement pratique...
Bj,
je plussoie sur ce qu'écrit Totor
Tous les poles sont simples et sont les racine m-ième de l'unité
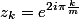
faudra surement distinguer selon la parité de m , car -1 est réel.
Après regrouper par par paire de poles conjugués, ce qui donne
des trinomes
)^2+sin^2(\frac{2 \pi k}{m}))
aux dénominateurs, à intégrer de prime abord, en log et arctan
je plussoie sur ce qu'écrit Totor
Tous les poles sont simples et sont les racine m-ième de l'unité
faudra surement distinguer selon la parité de m , car -1 est réel.
Après regrouper par par paire de poles conjugués, ce qui donne
des trinomes
aux dénominateurs, à intégrer de prime abord, en log et arctan
Effectivement, sauf pour des valeurs particulières des paramètres, cette intégrale ne s'exprime pas avec un nombre fini de fonctions élémentaires.
Par contre, il n'y a aucune difficulté à donner son expression analytique en faisant appel à une fonction spéciale. En effet, c'est une intégrale du genre hypergéométrique de Gauss. Et même plus simple que cela, car il s'agit de fonctions hypergéométriques particulières : on peut l'exprimer grâce la fonction "Beta incomplète".
Mais de toute façon, on en revient quand même à du calcul numérique, soit en intégrant directement, soit pour calculer numériquement la fonction spéciale utilisée.
Remarque : Pour certaines valeurs particulières des paramètres, la fonction Beta incomplète se réduit à diverses fonctions de niveau moins élevé, voire même à des polynômes dans certains cas.
Par contre, il n'y a aucune difficulté à donner son expression analytique en faisant appel à une fonction spéciale. En effet, c'est une intégrale du genre hypergéométrique de Gauss. Et même plus simple que cela, car il s'agit de fonctions hypergéométriques particulières : on peut l'exprimer grâce la fonction "Beta incomplète".
Mais de toute façon, on en revient quand même à du calcul numérique, soit en intégrant directement, soit pour calculer numériquement la fonction spéciale utilisée.
Remarque : Pour certaines valeurs particulières des paramètres, la fonction Beta incomplète se réduit à diverses fonctions de niveau moins élevé, voire même à des polynômes dans certains cas.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
