Un exo de topologie assez " hard " !

[Anonyme]

Bonsoir !
Voici petit exo de topologie qui me donne un peu de fil à retordre :
Soit f une fonction polynomiale non constante de C dans C .
1 - Montrer que l'image par f d'un fermé est un fermé.
2 - Montrer que l'image par f d'un ouvert est un ouvert .

J'ai trouvé la solution à la première question, mais je butte sur la seconde ...
Si vous avez du temps à perdre pour y jeter un petit coup d'oeil ...

Merci en tout cas !!

[Mike_51]

par curiosité, comment réponds-tu à la 1ère question stp

[Anonyme]

Pour la première question, je pense que le raisonnement suivant convient :
. On commence par démontrer que si A est une partie bornée de C, alors f-1 ( A ) aussi : c'est assez rapide !
. Ensuite, on peut considérer une suite convergente de l'ensemble f(F) ( F est le fermé de l'énoncé ) , que l'on écrit sous la forme ( f ( xn ) ) ( désolé pour les indices ... ) , ( où ( xn ) est donc une suite de F ) . Comme la suite ( f ( xn ) ) converge, elle est incluse dans un ensemble borné A . Donc ( xn ) est une suite de l'ensemble f -1 ( A ) , qui est lui-aussi borné d'après le premier point. D'après le th. de Bolzano - Weierstrass, ( xn ) admet une valeur d'adhérence , qui appartient à F, come celui-ci est fermé . ( f ( xn ) ) admet donc une valeur d'adhérence dans f ( A ) . Comme elle est convergente, elle converge donc vers cette valeur d'adhérence, donc vers un élément de f(A), donc de f(F) .
Toute suite convergente de f ( F ) converge donc dans f ( F ) et f ( F ) est fermé .

[El_Gato]

Salut,

f est dérivable (au sens complexe) et il n'y a qu'un nombre fini de points où la dérivée f' s'annule. Par le théorème d'inversion locale version analytique, dans , f est donc un difféomorphisme local bi-analytique sur son domaine de définition moins un nombre fini de points. Un difféomorphisme local est toujours une application ouverte (je crois, et c'est facile à montrer). On devrait pouvoir finir assez vite dans cette direction.

[yos]

Bon j'ai pas réfléchi à la question mais ce que tu dis El gato me semble faux : un difféo et même un homéo est une application ouverte par définition, mais l'adjectif local gâche tout ici.

[El_Gato]

Bon j'ai pas réfléchi à la question mais ce que tu dis El gato me semble faux : un difféo et même un homéo est une application ouverte par définition, mais l'adjectif local gâche tout ici.

Soit un homéomorphisme local d'un espace topologique X dans un autre top. Y. Soit U un ouvert de X, et . Si est tel que f(x)=y, il existe un ouvert W assez petit, localement autour de x, tel que W soit inclus dans U et f homéo de W sur f(W). Puisque W est inclus dans U, f(W) est un ouvert inclus dans f(U). Donc f(U) est un voisinage de chacun de ses points: f(U) est ouvert.

[yos]

Pour le théorème d'inversion locale, on a besoin que la dérivée ne s'annule pas. Que fait-on au voisinage d'un tel point?

[El_Gato]

Pour le théorème d'inversion locale, on a besoin que la dérivée ne s'annule pas. Que fait-on au voisinage d'un tel point?

Mon dernier post c'était pour montrer qu'un homéomorphisme local est bien une application ouverte.

Pour revenir à l'exo en question, soit n le degré de f, U un ouvert du plan complexe et z dans f(U). Alors f a n antécédents. Si l'un de ces antécédents n'annule pas la dérivée, alors f est un difféomorphisme local entre un voisinage de cet antécédent et le point z. Donc f est bien un difféomorphisme local dans ce cas là. Si tous les antécédents annulent la dérivée, on est plus ennuyé...

[Anonyme]

Salut et merci pour tes réponses ..
Mais ... à mon avis, la difficulté de l'exercice se situe bien lorsque l'on se place au voisinage d'un point annulant la dérivée de f.
De plus, tous les antécédents de x appartenant à f ( U ) n'appartiennent pas nécessairement à U, mais plus justement à f-1(f(U)) ...
Le mystère demeure ...!

[El_Gato]

Donc voici une solution complète.

1) Si f est une fonction définie sur un ouvert et si 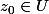est un point en lequel f est dérivable et de dérivée non nulle, il existe un ouvert tel que soit un homéomorphisme (et même un difféomorphisme).
Preuve: il suffit de recopier la démonstration du théorème des fonctions inverses dans le cas réel.

2) Si f est un homéomorphisme local sur U (c'est à dire que pour tout z dans U, il existe un voisinage ouvert tel que soit un homéomorphisme), alors f est une application ouverte sur U: l'image par f de tout ouvert inclus dans U est un ouvert.
Preuve: il suffit de recopier la preuve donnée dans le post ci-dessus (écrite pour des espaces topologiques quelconques, mais qu'on recopie sans difficulté dans le cas de ).

3) Soit f un polynôme et U un ouvert du plan complexe. Considérons . Si 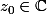est un antécédent de z tel que , f est un homéomorphisme local au voisinage de (que appartienne à U ou pas n'a pas d'importance). Supposons maintenant et 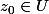. Comme f est continue, . Il n'y a qu'un nombre fini de tels points et f(U) moins un nombre fini de points adhérents est ouvert: dans f(U) est ouvert.

[Anonyme]

Merci beaucoup pour ta réponse !!
Seulement ... je ne vois pas ce qui te permet de dire que si f(U) moins un nombre fini de points d'adhérence est ouvert, alors f(U) est ouvert ...
Pourrais-tu développer un petit peu ce point ?
Merci encore !!

[El_Gato]

je ne vois pas ce qui te permet de dire que si f(U) moins un nombre fini de points d'adhérence est ouvert, alors f(U) est ouvert
Pourrais-tu développer un petit peu ce point ?

Oui c'est pas encore donné: si on prend pour f(U) le disque unité ouvert et pour z le point 1 par exemple. Je vais essayer de trouver du temps pour voir...

[El_Gato]

Donc reprenons. Le seul cas qui pose problème est le suivant: U ouvert, 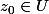avec et . Localement autour de f(z) s'écrit: où est un polynôme dont la dérivée ne s'annule pas en . Par le théorème d'inversion locale, appliqué à on peut inverser localement autour de : par un difféo local qui permet d'écrire localement f dans cette nouvelle carte . Cette application est bien ouverte au voisinage de .

Bon ca devient compliqué tout çà, je me demande s'il n'y a pas une solution plus simple en fait. Mais je ne la vois pas...

[yos]

f(U) moins un nombre fini de points adhérents est ouvert: dans f(U) est ouvert.

Ya une raison spéciale à ça? Parce qu'en général c'est faux. Un disque ouvert moins un point n'est plus ouvert par exemple. Mais j'ai lu en diagonale. Peut-être que je n'ai pas vu l'argument qui fait que ça marche ici.

[isortoq]

Bonsoir !

Soit f une fonction polynomiale non constante de C dans C .

2 - Montrer que l'image par f d'un ouvert est un ouvert .

On peut faire ça "à la main"...Et sans perte de généralité on peut supposer que le coef dominant de f est 1.
On prend b=f(a) dans f(A) ; comme A est ouvert, il existe r>0 tel que le disque ouvert D(a,r) est inclus ds A ; on considère ensuite V=D(b,r^n) où n est le degré du polynôme f et on montre que V est inclus ds f(A) ; pour cela on prend y ds V, et on regarde le polynôme : P(z)=f(z+a)-y ; il admet n racines z1,.., zn dont le produit est égal au terme constant de
P, i.e. P(0)=f(a)-y=b-y. En regardant les modules on voit que nécessairement une des racines zi a un module inférieur à r ; d'où x=a+zi est dans D(a,r) donc dans A et b=f(x)...

Voilà, voilà...

[quinto]

Un disque ouvert moins un point n'est plus ouvert par exemple.

En es tu sur?

[Anonyme]

par curiosité, est ce que la topologie figure au programme de sup???si oui, en quelle periode de l'année nous allons aborder ce genre d'exos!!!??
merci

[yos]

En es tu sur?

J'ai dit une bétise.

[quinto]

Oui, en fait il reste toujours ouvert.
Ne confonds tu pas avec fermé?
Un disque fermé moins un point n'est plus fermé.

[yos]

Il est clair qu'un ouvert moins un point est un ouvert car c'est l'intersection de deux ouverts :. J'ai dit n'importe quoi en voulant contester la méthode d'ElGato que je ne comprends toujours pas :

3) Soit f un polynôme et U un ouvert du plan complexe. Considérons . Si est un antécédent de z tel que , f est un homéomorphisme local au voisinage de (que appartienne à U ou pas n'a pas d'importance). Supposons maintenant et . Comme f est continue, . Il n'y a qu'un nombre fini de tels points et f(U) moins un nombre fini de points adhérents est ouvert: dans f(U) est ouvert.

Le cas est le seul qui pose problème. L'idée que j'entrevois est que on peut prendre 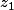aussi proche qu'on veut de et tel que (car les zéros sont isolés). Ensuite appliquer à 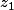le th. d'inversion locale : on aura un ouvert W contenant et un ouvert V contenant 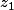homéomorphes. Si , ce sera gagné, mais je ne vois pas de raison simple à ça.
Je pense qu'il y a un truc à faire dans cette direction car ce qu'on doit prouver est un cas particulier du théorème de l'application ouverte pour les fonctions analytiques.
Pour le cas qui nous occupe (les polynômes), la solution d'isortoq est complète : l'idée est, il me semble, qu'un polynôme complexe non constant est surjectif (en vertu du th. de D'Alembert-Gauss). Du coup les complexes voisins de ont des antécédents, et ce qui fait marcher le truc c'est que l'un au moins des n antécédents d'un tel complexe est dans une boule centrée en et de rayon fixe (indépendant du voisin de considéré).