Limite d'une fonction quotient de fonction trigonométriques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 23 Aoû 2010, 21:45
par plums » 23 Aoû 2010, 21:45
Bonsoir !
J'aurais besoin d'aide, au moins une piste, sur la méthode pour calculer la limite de cette fonction en pi/6, je planche dessus depuis un bon bout de temps mais rien...
 = {tan(x)sin(x) - sin(x) \over 1 - 2sin(x)})
:help:
Merci !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2010, 22:03
par girdav » 23 Aoû 2010, 22:03
Bonjour,
on peut poser
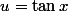
. Comme
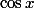
est positif au voisinage de
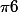
, on doit évaluer
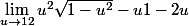
.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 23 Aoû 2010, 22:06
par Finrod » 23 Aoû 2010, 22:06
Une idée que je n'ai pas vérifié encore :
Prendre
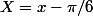
et faire la limite quand X tend vers zéro.
C'est bourrin...
sinon, un dl comme propose girdav.
 par busard_des_roseaux » 23 Aoû 2010, 23:16
par busard_des_roseaux » 23 Aoû 2010, 23:16
plums a écrit:Bonsoir !
J'aurais besoin d'aide, au moins une piste, sur la méthode pour calculer la limite de cette fonction en pi/6, je planche dessus depuis un bon bout de temps mais rien...
 = {tan(x)sin(x) - sin(x) \over 1 - 2sin(x)})
:help:
Merci !
Salut,
le numérateur a pour limite
 <0)
Le dénominateur est une fonction décroissante au voisinage de
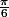
quand x tend vers
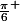
en diminuant
le dénominateur tend vers
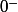
en augmentant.
PS: Quand la fonction est décroissante (comme
)
au voisinage de pi/6) : les quantités x et y=d(x) varient en sens inverse:
si x "décroit" vers
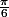
, alors d(x) "croit" vers 0.
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 11:05
par plums » 24 Aoû 2010, 11:05
Tout d'abord merci pour vos réponses!
Mais en réalité je me suis trompé : il y a des questions avant dans l'exercice qui permette de déduire la fonction a étudier, je vous ai donné celle que j'avais trouvé au début, mais j'avais fait des erreurs j'avais oublié un racine de 3. Bref tout ça pour dire que la fonction dont je n'arrive pas à trouver la limite est en fait
 = {\sqrt3 tan(x)sin(x) - sin(x) \over \sqrt3(1-2sin(x))})
Désolée pour l'erreur :wrong:
girdav a écrit:Bonjour,
on peut poser
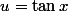
. Comme
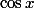
est positif au voisinage de
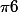
, on doit évaluer
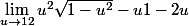
.
Je suppose que c'est en réalité
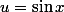
qu'il faut poser !
alors j'arrive donc à
})
mais ensuite je ne sais pas comment m'en sortir...?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 24 Aoû 2010, 11:45
par Euler07 » 24 Aoû 2010, 11:45
t'as utilisé la méthode de Bioche ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Aoû 2010, 11:53
par Doraki » 24 Aoû 2010, 11:53
f(x) = (-sin(x)/2) * (tan(x)-tan(pi/6)) / (sin(x)-sin(pi/6)) ?
 par busard_des_roseaux » 24 Aoû 2010, 12:02
par busard_des_roseaux » 24 Aoû 2010, 12:02
Bonjour,
on factorise pour distinguer ce qui s'annule des autres facteurs
= \frac{\sqrt{3} sin(x)}{ - \frac{\sqrt{3}}{2}} \, \frac{tan(x) - \frac{1}{\sqrt{3}}}{sin(x) - \frac{1}{2}})
Le 1er quotient a pour limite -1 (no problemo)
On divise ,haut et bas, le deuxième quotient par
)
pour faire apparaitre la limite comme quotient de deux "nombre dérivés"
})
c'est la règle de l'Hospital
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2010, 12:09
par girdav » 24 Aoû 2010, 12:09
plums a écrit:Je suppose que c'est en réalité
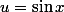
qu'il faut poser !
alors j'arrive donc à
})
mais ensuite je ne sais pas comment m'en sortir...?
Oui, c'est une faute de frappe. Regarde la limite du numérateur.
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 13:19
par plums » 24 Aoû 2010, 13:19
Euler 07 a écrit:t'as utilisé la méthode de Bioche ?
euh non...
Doraki a écrit:f(x) = (-sin(x)/2) * (tan(x)-tan(pi/6)) / (sin(x)-sin(pi/6)) ?
je ne vois pas comment tu arrives à ce résultat ?
girdav a écrit:Oui, c'est une faute de frappe. Regarde la limite du numérateur.
Je trouve 0....
busard_des_roseaux a écrit:Bonjour,
on factorise pour distinguer ce qui s'annule des autres facteurs
= \frac{\sqrt{3} sin(x)}{ - \frac{\sqrt{3}}{2}} \, \frac{tan(x) - \frac{1}{\sqrt{3}}}{sin(x) - \frac{1}{2}})
Le 1er quotient a pour limite -1 (no problemo)
On divise ,haut et bas, le deuxième quotient par
)
pour faire apparaitre la limite comme quotient de deux "nombre dérivés"
})
c'est la règle de l'Hospital
Merciiii ! je ne connaissais pas cette règle...
Il y a seulement une petite erreur il me semble, c'est
= \frac{\sqrt{3} sin(x)}{-2\sqrt{3}} \, \frac{tan(x) - \frac{1}{\sqrt{3}}}{sin(x) - \frac{1}{2}})
Je trouve donc
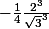
c'est à dire
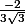
C'est OK ?
 par busard_des_roseaux » 24 Aoû 2010, 13:28
par busard_des_roseaux » 24 Aoû 2010, 13:28
plums a écrit:Il y a seulement une petite erreur il me semble, c'est
= \frac{\sqrt{3} sin(x)}{-2\sqrt{3}} \, \frac{tan(x) - \frac{1}{\sqrt{3}}}{sin(x) - \frac{1}{2}})
Je trouve donc
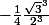
càd
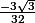
C'est OK ?
pour le -1/4 oui. sinon, pour le cube, c'est l'inverse :doh:
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 16:48
par plums » 24 Aoû 2010, 16:48
busard_des_roseaux a écrit:pour le -1/4 oui. sinon, pour le cube, c'est l'inverse :doh:
Autant pour moi !!
Merci beaucoup

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
. Comme
est positif au voisinage de
, on doit évaluer
.