Bonsoir !
J'ai besoin d'un petit coup de main concernant une question d'un exo, ça fait des heures que je tourne en rond ...
Enoncé :On suppose

un polynôme scindé à racines simples

distinctes .
1) Donner la DES de
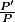
Pour ça aucun soucis, par calcul direct on trouve
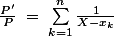
2) Montrer que P' admet n-1 racines simples

et que :

Ca j'ai un peu cherché, mais j'ai trouvé, on identifie P à la fonction polynomiale p, et en se plaçant sur un intervalle

,
 = p(x_{i+1}) = 0)
, p continue et dérivable sur

, On invoque le théorème de Rolle qui nous confirme l'existence d'au moins une racine de p' sur

, par suite il y a n-1 intervalles à considérer et puisque p n'est jamais constant sur l'un d'eux et que p' a obligatoirement n-1 racines (degré n-1), on en déduit l'unicité de la racine de p' dans l'intervalle

considéré.
Bon jusqu'ici ça allait. Et là je coince :
3) On pose
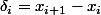
, montrer que :

indication : on pourra utiliser la question 1
J'ai dû essayer tout ce que je pouvais faire concernant

, j'ai rien trouvé (j'ai essayer de le retourner dans tous les sens, de le dériver, de majorer tout ce que je pouvais, résultat = rien). Ensuite j'ai essayé sans utiliser 1), à savoir montrer que éventuellement
 = P(x_{i+1} - \frac{\delta_i}{n} ))
pour réinvoquer Rolle, j'ai essayé en calculant l'équation de la tangente en
)
et en
 ))
afin de calculer le point d'intersection des deux, et encadrer mieux le

, j'ai essayé en construisant le polynôme du second degré tel que
 = 0)
et que
=0)
pour trouver des relation entre les

et les

, j'ai tenter la méthode de Newton sur P' pour encadrer les racines plus près, enfin bref plus ça va et plus je m'engage dans des trucs qui n'ont aucunes chances d'aboutir ....
Je n'arrive à voir le raisonnement, le théorème ou la propriété clé pour prouver le résultat ... Je n'arrive pas à voir d'où peut venir le n au dénominateur du delta (comment mêler le degré de P avec les racines ??? ou comment pourrait il venir de la somme de la DES de
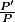
??? ) ... Et comment utiliser cette DES ???
Bref après moult idées non-abouties je déclare forfait ...
Quelqu'un peut il me donner un indice supplémentaire ? (pas me donner la réponse directement mais un indice) ...
Merci
