Arithmétique

par **Dinozzo13** » 18 Aoû 2010, 21:09

Salut ! Je propose un petit exo sympa :

Soient

tels que

.
Montrer que

est un carré parfait.

Amusez-vous bien

par **Zweig** » 18 Aoû 2010, 22:29

Humm, j'avais déjà fait cet exercice, j'avais utilisé une "formule magique" que je n'arrive plus à retrouver en tâtonnant :cry:

par **Zweig** » 18 Aoû 2010, 22:33

La relation se réécrit (m-n)(1+4(m+n)) = m^2, ça ne me semble pas celle que j'avais trouvée à l'époque ...

par **Dinozzo13** » 18 Aoû 2010, 22:34

Je donne une petite indication pour ceux qui le désire :++:
Poser d=PGCD(m,n) et n=da et m=db

par **stevi** » 19 Aoû 2010, 00:21

salut
zweig cela na po besoin d'aucune formule magik!!

lorsque tu as (m-n)(3(m+m)+1)=n² on note par d le pgcd de m et n
et puis tu remplace m= da et n=db ou a et b premiers entre eux o aura apré
(a-b)(3d(a+b)+1)=d b² puiske a-b et b² sont premiers entre eux alors a-b divise d et comme on a d premier avec 3d(a+b)+1 alors d divise a-b et donc a-b= d et donc m-n=d²

stevi

par **Ben314** » 19 Aoû 2010, 01:01

Salut,
Si on veut, on peut aussi se passer du pgcd :
Si

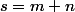
alors

implique que

maizaussi que

.
On a donc

ce qui montre que

est un carré parfait et donc que

et

sont des carrés parfaits vu qu'il sont premiers entre eux.
A l'aide d'une des deux premières formules, on en déduit bien que

est lui aussi un carré parfait.

par **Dinozzo13** » 19 Aoû 2010, 01:42

... Tu m'impressionneras toujours ^^
(Fais moi signe quand tu caleras :ptdr:)

@Stevi : Bien joué, j'ai adopté le même raisonnment :++:

Arithmétique

arithmétique

Qui est en ligne