Développement limité en 0+
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 17 Aoû 2010, 19:54
par plums » 17 Aoû 2010, 19:54
Bonsoir à tous !
J'ai une question en ce qui concerne un calcul de développement limité :
on me demande de déterminer le DL de
})
en 0+.
Ce n'est pas surprenant puisque cette fonction n'est pas définie en 0. Je n'ai jamais étudier de DL en 0+ je n'ai aucune idée de comment m'y prendre...!
Une petite aide pour démarrer ne serait pas de refus !
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 17 Aoû 2010, 21:36
par dibeteriou » 17 Aoû 2010, 21:36
Classiquement, tu peux chercher le DL0 de
)
par intégration (de quoi ?) puis composer.
Ensuite, l'un des facteurs du dénominateur va se simplifier.
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 17 Aoû 2010, 21:38
par plums » 17 Aoû 2010, 21:38
dibeteriou a écrit:Classiquement, tu peux chercher le DL0 de
)
par intégration (de quoi ?) puis composer.
Ensuite, l'un des facteurs du dénominateur va se simplifier.
Merci pour ta réponse mais ça c'est pour un DL0 classique ! Ca ne change rien que ça soit en D en 0+ ?
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 17 Aoû 2010, 21:40
par dibeteriou » 17 Aoû 2010, 21:40
Non.
Un DL, c'est une approximation.
Si elle est valable au voisinage de 0, ça l'est sur un voisinage de 0+ (qui apparaît quand tu composes ton DL...).
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 17 Aoû 2010, 21:47
par plums » 17 Aoû 2010, 21:47
D'accord, c'était simplement ma question. :)
Merci bien !
-
mathelot
 par mathelot » 17 Aoû 2010, 22:10
par mathelot » 17 Aoû 2010, 22:10
dibeteriou a écrit:Classiquement, tu peux chercher le DL0 de
)
par intégration (de quoi ?) puis composer.
Ensuite, l'un des facteurs du dénominateur va se simplifier.
Bonsoir,
c'est "bien" ce qui est conseillé. :we:
remarque :
en posant
=\sqrt{x})
={2u \over |sin(2u)|})
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 18 Aoû 2010, 14:12
par plums » 18 Aoû 2010, 14:12
Merci ! ça sera plus simple si j'effectue ce changement de variable ?
Alors sinon, j'ai plusieurs problèmes.
tout d'abord par 2 méthodes différentes je ne trouve pas le même résultat pour arcin (je développe surement à un ordre trop grand, mais je voudrais savoir quand même ou se situe mon erreur).
 = {1 \over\ sqrt{1-x^2}}=(1-x^2)^{-1/2}=1 + {\fr12}x^2 + {\fr38}x^4)
Donc
 = x + {x^3 \over\6} + {3x^5 \over\ {40}})
Mais en faisant :
 = {1 \over\ 1-1+(1-x^2)^{1/2}})
Comme
^{1/2} = -{\fr12}x^2)
et

, on a
 = 1 + {\fr12}x^2 + {\fr18}x^4)
...
Bon en regardant sur internet j'ai vu que la bonne solution était la première.
Ensuite je trouve

et donc
 = \fr38 + \fr34x - \fr18x^2)
... ?
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 18 Aoû 2010, 14:34
par plums » 18 Aoû 2010, 14:34
Finalement j'ai trouvé quelque chose en simplifiant avec le dénominateur en effet... :

Je ne suis pas du tout sûre de moi ...!
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 20 Aoû 2010, 09:22
par plums » 20 Aoû 2010, 09:22
Up... :girl2:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 20 Aoû 2010, 10:48
par Ericovitchi » 20 Aoû 2010, 10:48
il faudrait trouver :
/3+(8 x^2)/15+(16 x^3)/35+(128 x^4)/315+(256 x^5)/693+(1024 x^6)/3003+O(x^{13/2}))
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 21:10
par plums » 24 Aoû 2010, 21:10
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Aoû 2010, 21:39
par Doraki » 24 Aoû 2010, 21:39
plums a écrit: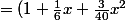 \frac1{1 - \frac12x - \frac18x^2})
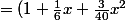 (1 + \frac12x + \frac18x^2})
1/(1-ax-bx²) ça fait pas 1+ax+bx²+O(x^3)
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 21:42
par plums » 24 Aoû 2010, 21:42
Doraki a écrit:1/(1-ax-bx²) ça fait pas 1+ax+bx²+O(x^3)
Ah bon ?
Pourtant

... non ?
:hein:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Aoû 2010, 22:38
par Doraki » 24 Aoû 2010, 22:38
Bah oui, 1/(1-u) = 1+u+u²+u^3+...
Ca fait pas 1+u.
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 24 Aoû 2010, 22:56
par plums » 24 Aoû 2010, 22:56
Doraki a écrit:Bah oui, 1/(1-u) = 1+u+u²+u^3+...
Ca fait pas 1+u.
Pff je fais vraiment n'importe quoi... :marteau: Merci !!!
C'est bon, j'arrive au bon résultat si je fais un DL du numérateur et du dénominateur à l'ordre 2.
Dernière chose, je n'obtiens pas ce qu'il faut si je le fais à l'ordre 1 :
})

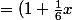 \frac{1}{1 - \frac12x})
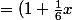 (1 + \frac12x + \frac14x^2})

C'est la dernière fois que je polue ce post promis !
-
plums
- Membre Naturel
- Messages: 22
- Enregistré le: 17 Aoû 2010, 09:53
-
 par plums » 25 Aoû 2010, 09:00
par plums » 25 Aoû 2010, 09:00
Doraki a écrit:Bah oui, 1/(1-u) = 1+u+u²+u^3+...
Ca fait pas 1+u.
Oui ok, bien sûr, j'ai trouvé mes erreurs, merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
