Somme des diviseurs d'un nombre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gagbill
- Messages: 6
- Enregistré le: 17 Aoû 2010, 19:48
-
 par Gagbill » 17 Aoû 2010, 20:54
par Gagbill » 17 Aoû 2010, 20:54
Bonjour, je souhaiterai avoir la démonstration de la formule de la somme des diviseurs d'un nombre entier.
En effet si on note
s(n) la somme d'un entier
n dont la décomposition en facteur premier est
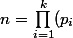^a^i)
, on a :
=(1+ p_1^1 + p_1^2 +...+ p_1^a1)\times(1+ p_2^1 + p_2^2 +...+ p_2^a2)\times...\times(1+ p_k^1 + p_k^2 +...+ p_k^ak))
.
C'est de ce produit dont j'aimerai obtenir la déduction logique, soit d'un lien, d'un document ou pourquoi pas de vos connaissances. Merci
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 17 Aoû 2010, 21:23
par dibeteriou » 17 Aoû 2010, 21:23
Bonjour.
Tu peux chercher dans la direction des fonctions arithmétiques multiplicatives.
On démontre (en particulier par convolution) que la fonction

dont tu parles est multiplicative, c'est à dire que si

et

sont premiers entre eux,
=\sigma(n)\sigma(m))
.
Ensuite on calcule simplement
}))
pour en déduire
)

edit: correction de la grosse erreur.
-
Gagbill
- Messages: 6
- Enregistré le: 17 Aoû 2010, 19:48
-
 par Gagbill » 18 Aoû 2010, 04:12
par Gagbill » 18 Aoû 2010, 04:12
dibeteriou a écrit:Tu peux chercher dans la direction des fonctions arithmétiques multiplicatives.
En effet, je vois maintenant que c'est la meilleure façon de démontrer cela. Thanks :ptdr:
si

et

sont premiers entre eux,
=\sigma(m))
.
Par contre, je pense ici que que c'est plutôt si

et

sont premiers entre eux, alors
=\sigma(n)\sigma(m))
Bref, voici la démonstration que j'ai concocté en suivant ton indication:
Montrons que ) est une fonction multiplicative
est une fonction multiplicative:
=1) (1 n'ayant qu'un diviseur, lui-même)
(1 n'ayant qu'un diviseur, lui-même)- Montrons que
=\sigma(m)\sigma(n)) avec
avec 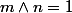
Par définition, =\sum_{d|n}d)
Considérons 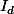 et
et  respectivement l'application identique (ex:
respectivement l'application identique (ex:=n) ) et la fonction arithmétique constante égale à 1 (ex:
) et la fonction arithmétique constante égale à 1 (ex:=1) ), on a:
), on a: (n)=\sum_{d|n} I_d(d)1(\frac{n}{d})) produit de convolution
produit de convolution
(n)=\sum_{d|n}d)
Par conséquent:=(I_d\star1)(n)) (i)
(i)
Soit \in \mathbb{N}^2) tels que
tels que 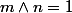 ; on a:
; on a:
(mn)=\sum_{d|mn} d)
Or  et
et  étant premier entre eux, 1 est leur seul diviseur commun; ainsi
étant premier entre eux, 1 est leur seul diviseur commun; ainsi \in \mathbb{N}^*\times \mathbb{N}^*) ,
, 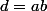 avec
avec 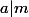 et
et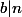
D'où (mn)=\sum_{a|m}\sum_{b|n} ab)
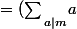 (\Big\sum_{b|m} b))
(mn)=(I_d \star 1)(m)(I_d \star 1)(n))
D'après la relation (i): =\sigma(m)\sigma(n))
[center]Conclusion: ) est une fonction multiplicative[/center]
est une fonction multiplicative[/center]
Déduisons )
De ce qui précède, =\sigma(p_1^a1)\sigma(p_2^a2)...\sigma(p_k^ak))
En s'intéressant en particulier ) , on a:
, on a:
Soit D l'ensemble des diviseurs de 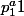 ; ainsi:
; ainsi:
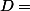 {
{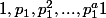 }
}
De manière analogue, on trouve l'ensemble des diviseurs de 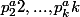
Donc =(1+p_1^1+p_1^2+...+p_1^a1)(1+p_2^1+p_2^2+...+p_2^a2)...(1+p_k^1+p_k^2+...+p_k^ak))
CONCLUSION:
=(1+p_1^1+p_1^2+...+p_1^a1)(1+p_2^1+p_2^2+...+p_2^a2)...(1+p_k^1+p_k^2+...+p_k^ak))
avec
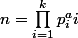
Voilà, n'hésitez pas à m'indiquer tout erreur, amélioration, astuce ou encore critique sur cette démonstration.
Cordialement et encore merci
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 18 Aoû 2010, 13:14
par dibeteriou » 18 Aoû 2010, 13:14
Merci pour la correction

C'est tout à fait la preuve classique. La convolution est un bon moyen d'obtenir des fonctions multiplicatives :we:
Il doit y avoir simplement une coquille à la dernière ligne, au niveau des puissances (
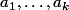
au lieu de

).
-
Gagbill
- Messages: 6
- Enregistré le: 17 Aoû 2010, 19:48
-
 par Gagbill » 18 Aoû 2010, 15:57
par Gagbill » 18 Aoû 2010, 15:57
dibeteriou a écrit:Il doit y avoir simplement une coquille à la dernière ligne, au niveau des puissances (
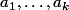
au lieu de

).
Tout à fait, manque de justesse niveau Latex :briques: . Bien aurevoir et encore merci :we:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Aoû 2010, 17:17
par girdav » 18 Aoû 2010, 17:17
Bonjour,
on peut aussi obtenir la formule en bourinant : la donnée d'un diviseur correspond à celle d'un élément de
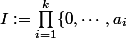
.
En notant la somme des diviseurs de

par
)
, on a :
&=\sum_{(x_1,\cdots,x_k\)\in I}\prod_{i=1}^k p_i^{x_i}\\<br />&= \sum_{l_1=1}^{a_1}\ldots\sum_{l_k=1}^{a_k}\prod_{i=1}^k p_i^{l_i}\\<br />&= \(\sum_{l_1 =1}^{a_1}p_1^{l_1}\)\ldots\(\sum_{l_k=1}^{a_k}p_k^{l_k}\),<br />\end{align})
la dernière égalité s'obtenant en regroupant les sommes (c'est une généralisation de la formule
\in A\times B}x_ay_b = \(\sum_{a\in A}x_a\)\(\sum_{b\in B}y_b\))
pour

et

finis).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 18 Aoû 2010, 18:37
par benekire2 » 18 Aoû 2010, 18:37
girdav a écrit:Bonjour,
on peut aussi obtenir la formule en bourinant : la donnée d'un diviseur correspond à celle d'un élément de
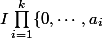
.
En notant la somme des diviseurs de

par
)
, on a :
&=\sum_{(x_1,\cdots,x_k\)\in I}\prod_{i=1}^k p_i^{x_i}\\<br />&= \sum_{l_1=1}^{a_1}\ldots\sum_{l_k=1}^{a_k}\prod_{i=1}^k p_i^{l_i}\\<br />&= \(\sum_{l_1 =1}^{a_1}p_1^{l_1}\)\ldots\(\sum_{l_k=1}^{a_k}p_k^{l_k}\),<br />\end{align})
la dernière égalité s'obtenant en regroupant les sommes (c'est une généralisation de la formule
\in A\times B}x_ay_b = \(\sum_{a\in A}x_a\)\(\sum_{b\in B}y_b\))
pour

et

finis).
Salut girdav !
C'est cette preuve qui figure dans les bouquins de TS ( datant d'il y a quelques années) en version bien plus romancée bien sûr
-
Gagbill
- Messages: 6
- Enregistré le: 17 Aoû 2010, 19:48
-
 par Gagbill » 18 Aoû 2010, 19:41
par Gagbill » 18 Aoû 2010, 19:41
girdav a écrit:Bonjour,
on peut aussi obtenir la formule en bourinant : la donnée d'un diviseur correspond à celle d'un élément de
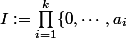
.
En notant la somme des diviseurs de

par
)
, on a :
&=\sum_{(x_1,\cdots,x_k\)\in I}\prod_{i=1}^k p_i^{x_i}\\<br />&= \sum_{l_1=1}^{a_1}\ldots\sum_{l_k=1}^{a_k}\prod_{i=1}^k p_i^{l_i}\\<br />&= \(\sum_{l_1 =1}^{a_1}p_1^{l_1}\)\ldots\(\sum_{l_k=1}^{a_k}p_k^{l_k}\),<br />\end{align})
la dernière égalité s'obtenant en regroupant les sommes (c'est une généralisation de la formule
\in A\times B}x_ay_b = \(\sum_{a\in A}x_a\)\(\sum_{b\in B}y_b\))
pour

et

finis).
Salut, je prends note aussi de cette démonstration, semble-t-elle, plus courte et astucieuse.
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
et
sont premiers entre eux,
.
.
par
, on a :
pour
et
finis).
.
par
, on a :
pour
et
finis).