Matrices

[girdav]

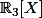
... puisque la dimension de est quatre.

[Mister Red]

Ah oui j'ai oublié de compter le degré nul. Puisque c'est quatre donc ker(f) est de dimension 1. Comment déterminer alors une base de ker(f) ?

[girdav]

Il suffit de trouver une vecteur non nul du noyau.
Méthode 1 :si on pose , quelle conditions a-t-on sur les constantes , , et ?
Méthode 2 : que donne l'image du dernier vecteur de la base canonique?

[Mister Red]

Méthode 1 : a,b,c et d sont des réels. Pas compris la méthode.

Méthode 2 : Le dernier vecteur de la base canonique est X^3. Son image par f est 3X²+X. Pour quoi choisit-on le dernier vecteur ?

[girdav]

Méthode 1 : a,b,c et d sont des réels. Pas compris la méthode.

On doit résoudre un système :

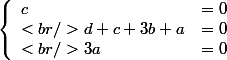
Méthode 2 : Le dernier vecteur de la base canonique est X^3. Son image par f est 3X²+X. Pour quoi choisit-on le dernier vecteur ?

Je me suis un peu enflammé en cette fin de journée. Le feeling ne marche pas si bien que ça.

[Mister Red]

ok on va rester sur la méthode 1. Simplement on n'a que trois équations pour quatre inconnues...

[girdav]

C'est normal : les solutions seront données à une constante multiplicative près.
Ceci n'a rien de scandaleux pour un sous-espace de dimension un.

[Mister Red]

Donc on aura a=0, c=0 et 3b +d=0. Le polynome s'écrit donc P(X)=bX²+d avec 3b+d=0

Une base de ker(f) serait donc (bX²+d) ?

[girdav]

Tu peux fixer une inconnue, par exemple ce qui donne .

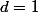
[Mister Red]

Pourquoi a-t-on le droit ?

[girdav]

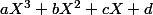
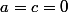
Tous les polynômes de la forme avec et sont dans le noyau, donc c'est vrai en particulier si (le choix de cette valeur n'est pas important, on peut prendre ).

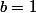
[Mister Red]

Ok d'accord merci Girdav ton aide m'a été très utile !