[L1] Encore un équivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 17:38
par benekire2 » 13 Aoû 2010, 17:38
Bonjour,
Je n'ai toujours pas résolu ma question précédente sur les équivalents, mais sur un autre exercice je rencontre un problème.
Il s'agit de donner un équivalent ( que l'on note u) en l'infini de
})
puis de donner un équivalent en l'infini de
} -u(x))
Et bien je n'arrive pas a faire la première partie ... quelqu'un pourrait il m'indiquer comment procéder ?
Merci beaucoup :id:
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 13 Aoû 2010, 17:54
par Pythales » 13 Aoû 2010, 17:54
Pour débloquer la situation :


^2}x+...)
(à rédiger)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 18:36
par benekire2 » 13 Aoû 2010, 18:36
Pour le développement de x^(1/x) oui pas de problèmes .. je vais y réfléchir pour la suite
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 13 Aoû 2010, 18:42
par Finrod » 13 Aoû 2010, 18:42
Pythales a écrit:
euh... j'ai
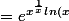} = e^{e^{\frac{ln(x)}{x}}ln(x)})
pour ln(u) j'ai pareil que toi
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 13 Aoû 2010, 18:47
par Pythales » 13 Aoû 2010, 18:47
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 13 Aoû 2010, 18:52
par Finrod » 13 Aoû 2010, 18:52
aaaaah c'était l'exp du dev limité du log :happy:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 19:17
par Nightmare » 13 Aoû 2010, 19:17
Ne pas oublier la notion d'approximation affine vue en première (et malheureusement pas du tout exploitée à ce niveau), qui peut être très utile lorsqu'il s'agit d'approcher localement des fonctions dérivables.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 21:12
par benekire2 » 13 Aoû 2010, 21:12
Alors je reprends depuis le début,
( mes égalités sont "à l'infini" )
Pour commencer
}{x}+o\(\frac{ln(x)}{x}\))
On a donc :
}{x}+o\(\frac{ln(x)}{x}\)}=xx^{\frac{ln(x)}{x}}e^{o\(\frac{ln(x)}{x}\)}})
Maintenant
=\ln(x)+\frac{(\ln(x))^2}{x}+o\(\frac{ln(x)}{x}\)})
Le meilleur équivalent que j'avais c'était
+x}{x}})
mais on peut faire largement mieux je pense ...
Maintenant, à quoi ça sert de savoir que ln(u) est équivalent à ln(x) ? Ca doit bien servir mais je vois pas trop ,
Merci :we:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 13 Aoû 2010, 21:47
par Finrod » 13 Aoû 2010, 21:47
L'équivalent est le premier terme non nul du dl, il est unique.
l'équivalent de ln(u) est simple, après il faut vérifier que on peut passer à l'exponentielle. Pour cela il faut que le second terme du dl tende vers 0, c'est le cas. (car l'exponentielle transforme la somme en produit donc il faut un facteur de 1.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 21:59
par benekire2 » 13 Aoû 2010, 21:59
Oui pour passer à l'exponentielle il faut que ln(x)-ln(u) -->0 je sais et donc du coup normalement un équivalent de u est x.
On cherche maintenant un équivalent de u-x, et je pense qu'un équivalent de cette "bête" est ln²(x) si je me trompe pas.
PS: Je remarque a quel point mon post précédent était con :doh:
-
get-27
- Messages: 9
- Enregistré le: 01 Fév 2009, 19:48
-
 par get-27 » 13 Aoû 2010, 22:45
par get-27 » 13 Aoû 2010, 22:45
Bah il faut pas faire un petit développement asymptotique ?
Pour x voisin de l'infini :
 }{x}} + \circ ({\frac {\ln \left( x \right) }{x}}))
Donc pour x tendant vers l'infini :
 }{x}} + \circ ({\frac {\ln \left( x \right) }{x}})} = e^{ln(x) + \frac{ln^2(x)}{x} + \circ(\frac{ln^2(x)}{x})} = x + ln^2(x) + \circ(ln^2(x)))
Tu réduit la précision et tu trouve que l'équivalent en l'infini est x.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 22:49
par benekire2 » 13 Aoû 2010, 22:49
C'est ce que j'ai fais , du moins ce que j'ai fini par faire ...
Merci vous tous :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Aoû 2010, 22:55
par benekire2 » 13 Aoû 2010, 22:55
Sinon, dans un DS de MPSI j'ai trouvé la question suivante :
Trouver la limite de la suite de terme général
...(n+n)})
J'ai conclu avec la formule de Stirling, sauf que je suis pas sûr que c'est un résultat au programme et de plus c'est une question indépendante et pas de démo de la formule de Stirling
Une autre méthode ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 23:03
par Nightmare » 13 Aoû 2010, 23:03
Passer au log puis écrire que
=ln(n)+ln\(1+\frac{k}{n}\))
semble marcher. On est ramener à calculer une somme de Riemann.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 14 Aoû 2010, 08:19
par benekire2 » 14 Aoû 2010, 08:19
ok, merci ! :we:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Aoû 2010, 10:49
par Nightmare » 14 Aoû 2010, 10:49
As-tu réussi ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 14 Aoû 2010, 11:50
par benekire2 » 14 Aoû 2010, 11:50
J'ai pas eu le temps ce matin ( déchetterie oblige ) et cet aprem je donne un cours, je verrai ce soir, mais comme ça de tête ça a l'air de bien réduire le truc. J'avais déj essayé de pasé au log ca avait rien donné, mais j'avais pas du tout pensé l'identité ln(n+k) [que je connais d'ailleurs ... ]
Je te tiens au courant.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
