Tétraèdre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 03 Aoû 2010, 17:36
par Phoenicia » 03 Aoû 2010, 17:36
Bonjour,
Soit ABCD un tétraèdre. M un point de l'arête [AD] et (;)) le plan passant par M et parallèle aux droites (AB) et (CD). (;)) coupe [AC] en N,[BC] en P et [BD] en Q.
I et J milieu respectifs des segments [AB] et [CD], K l'intersection de [MP] et [QN]
La question:
Soit x l'abcisse de M dans le repère (A,

)
Démontrez que
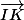
=
x 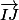


-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 03 Aoû 2010, 19:14
par Hiphigenie » 03 Aoû 2010, 19:14
Bonjour,
En décomposant
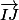
de deux manières différentes, tu peux démontrer que

En décomposant
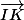
de deux manières différentes, tu peux démontrer que

(à condition d'avoir démontré que MNPQ est un parallélogramme)
Tu sais que

.
Tu peux démontrer que

par Thalès.
D'où...
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 16:58
par Phoenicia » 04 Aoû 2010, 16:58

C'est une formule qu'on doit apprendre par coeur ou il faut le déduire? :happy2:

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 17:07
par Hiphigenie » 04 Aoû 2010, 17:07
Phoenicia a écrit:Soit x l'abcisse de M dans le repère (A,

)
Cela veut dire quoi, selon toi ?
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 19:32
par Phoenicia » 04 Aoû 2010, 19:32
J'ai appris que c'est un vecteur directeur de M mais je crois que j'ai pas bien compris :hein:
Et pourquoi doit on démontrer que

? Je comprend pas trop le raisonnement, merci

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 19:48
par Hiphigenie » 04 Aoû 2010, 19:48
Parce que, si tu remets tout ensemble, tu as :



.

Tu en déduis que
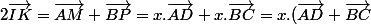 = x.(2\vec{IJ}) = 2(x\vec{IJ}))
Donc, si on a :
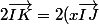)
, tu en déduis bien que

.
C'était bien ce qu'il fallait démontrer...
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 19:51
par Phoenicia » 04 Aoû 2010, 19:51
Vecteur AD veut bien dire vecteur directeur de M?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 19:54
par Hiphigenie » 04 Aoû 2010, 19:54
Phoenicia a écrit:Vecteur AD veut bien dire vecteur directeur de M?
C'est le vecteur unitaire.
Que veux-tu dire par le vecteur directeur d'un point ?
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 19:57
par Phoenicia » 04 Aoû 2010, 19:57
C'est pas comme le vecteur directeur d'une droite?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 19:59
par Hiphigenie » 04 Aoû 2010, 19:59

est un vecteur directeur de la droite passant par A et par D.
OK !
Mais ce n'est pas un vecteur directeur d'un point ...

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 20:01
par Hiphigenie » 04 Aoû 2010, 20:01

est un vecteur unitaire. C'est un vecteur de longueur égale à 1.
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 20:01
par Phoenicia » 04 Aoû 2010, 20:01
Est-ce que c'est la méthode la plus courte?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 20:03
par Hiphigenie » 04 Aoû 2010, 20:03
A chacun son point de vue, mais je ne trouve pas cette méthode longue. :id:

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Aoû 2010, 20:04
par Hiphigenie » 04 Aoû 2010, 20:04
Un petit peu de Chasles, un petit peu de Thalès et oups...
-
Phoenicia
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Mar 2010, 20:41
-
 par Phoenicia » 04 Aoû 2010, 20:40
par Phoenicia » 04 Aoû 2010, 20:40
Juste une précision pour

l'étape d'après on cherche à mettre en relation les vecteurs de chaque :AD avec AM BC avec BP?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités

