Merci de ta réponse.
Effectivement, je me suis trompé pour le cas n=2. Si on prend pour
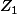
une distribution d'espérance maximale, alors forcément, la distribution de
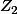
sera d'espérance minimale puisque:
\mathbb{E}[Z_2]=1)
Donc pour
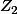
, il faut prendre:
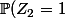 = 1-\pi_1)
et
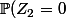 = \pi_1)
En ce qui concerne l'indépendance des variables
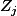
, elles ne le sont pas (compte tenu du problème d'où vient cette question de maths). Et même si j'en faisais l'hypothèse, avec la relation
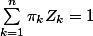
, on aurait de toute façon au mieux "n-1 degrés de liberté".
Pour ta remarque sur les lois, je ne la comprends pas trop puisque les lois des variables, c'est justement à moi de les choisir de façon judicieuse pour maximiser l'espérance d'un des
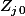
, les autres étant à fixer de façon à respecter les contraintes et à permettre à l'espérance de
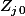
d'être maximisée (oui j'ai changé l'objectif par rapport à hier puisque ta remarque m'a montré que maximiser tout le monde à la fois ne marche pas).
L'objectif est donc de trouver pour un
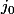
fixé, la borne sup de
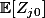
dans le cas où n est quelconque.
p.s: les
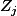
sont des variables à densité donc leur proba en 1 point est forcément nulle, mais c'est un abus de langage: il faut plutôt voir
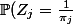 = \pi_j)
comme
 = \pi_j)
avec delta aussi petit que l'on veux.
