Racine carrée [3ème]
Réponses à toutes vos questions du CP à la 3ème
-
mathelot
 par mathelot » 21 Juil 2010, 17:51
par mathelot » 21 Juil 2010, 17:51
Bonjour,
voilà un petit exercice sans prétention
simplifier

@+

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 21 Juil 2010, 19:03
par Lostounet » 21 Juil 2010, 19:03
Salut! C'est intéressant ça..!
Faudrait justement en profiter pour proposer un truc du genre:
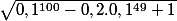
Pour que la simplification ne se fasse pas facilement :zen:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
tacotac
- Messages: 6
- Enregistré le: 11 Fév 2010, 15:24
-
 par tacotac » 21 Juil 2010, 19:24
par tacotac » 21 Juil 2010, 19:24
et bien prend ta calculette et calcule : ce qui te donne en dessous de la racine 126765060022823165329651689025 ( ce qui est assez considérable ) .... et aprés tu essayes de le mettre sous la forme de a racine b

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 21 Juil 2010, 19:32
par Lostounet » 21 Juil 2010, 19:32
:ptdr: :ptdr:
Il y a un peu plus simple quand même..!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Sve@r
 par Sve@r » 22 Juil 2010, 10:18
par Sve@r » 22 Juil 2010, 10:18
tacotac a écrit:et bien prend ta calculette et calcule
Dans ce genre d'exercice, on demande surtout de faire preuve de finesse et d'astuce plutôt que d'aller appuyer sur les touches d'un cerveau de remplacement (qui, d'ailleurs, ne sera jamais aussi performant que le tien)
tacotac a écrit: ce qui te donne en dessous de la racine 126765060022823165329651689025 ( ce qui est assez considérable ) .... et aprés tu essayes de le mettre sous la forme de a racine b
Bon courage. Surtout quand on connait le résultat de l'expression. Avec un bon stylo tu en auras pour quelques dizaines d'années...
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 22 Juil 2010, 15:44
par oscar » 22 Juil 2010, 15:44
Il suffit de faire apparaître un carré parfait a²+2ab +b²
2 ^ 100 + 2 ^51 + 1=

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 22 Juil 2010, 19:09
par Hiphigenie » 22 Juil 2010, 19:09
mathelot a écrit:
Bonjour,
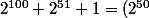^2 + 2.2^{50} + 1)
Si
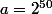
, alors
^2 + 2.2^{50} + 1 = a^2+2a+1)
.
Cela ne te fait penser à rien ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 19:20
par Lostounet » 22 Juil 2010, 19:20
Hiphigenie a écrit:Cela ne te fait penser à rien ?
Sauf que mathelot est prof de maths aussi :ptdr:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 22 Juil 2010, 19:58
par mathelot » 22 Juil 2010, 19:58
celle-là , par contre, est-elle faisable au collège ?

je ne pense pas :hein:
celle-là ?

:hein:
celle-là !!
^{2010}+(\sqrt{2}-1)^{-2010}})
:ptdr:

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 22 Juil 2010, 20:03
par Hiphigenie » 22 Juil 2010, 20:03
Lostounet a écrit:Sauf que mathelot est prof de maths aussi :ptdr:
Oh ! Pardon ! Je n'avais pas compris l'astuce du post... :triste:
Désolé pour la méprise et, en plus, j'ai l'air ridicule :happy2:
-
Sve@r
 par Sve@r » 22 Juil 2010, 20:33
par Sve@r » 22 Juil 2010, 20:33
mathelot a écrit: celle-là ?

:hein:
Celle-là ça se fait de tête. Les 2 autres... :marteau:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 20:50
par Lostounet » 22 Juil 2010, 20:50
Salut,
Oui la deuxième se fait à la tête, tu aurais du poser un truc négatif ou il faut comparer et mettre un (-1)..! Je trouve ça magnifique (et utile pour truquer des élèves aux connaissances fragiles)
La dernière.. j'obtiens une malheureuse fraction avec un dénominateur irrationnel^1005 (C'est bien qu'on est en 2010 et non en 2009) :marteau:
EDIT: Euh non, j'ai fait une petite erreur mais bon, je pense que c'est pareil..
Pour la première je vais chercher ;)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 24 Aoû 2010, 13:00
par mathelot » 24 Aoû 2010, 13:00
-
mathelot
 par mathelot » 24 Aoû 2010, 13:03
par mathelot » 24 Aoû 2010, 13:03
-
mathelot
 par mathelot » 25 Aoû 2010, 09:39
par mathelot » 25 Aoû 2010, 09:39
Bj,
Simplifier
 \, \left( \frac{ 2^{2010}+1 }{\sqrt{2}} \right) +1})
:we:
@+
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 25 Aoû 2010, 19:38
par nodjim » 25 Aoû 2010, 19:38
C'est une question pour les bons collégiens.
-
mathelot
 par mathelot » 25 Aoû 2010, 22:13
par mathelot » 25 Aoû 2010, 22:13
nodjim a écrit:C'est une question pour les bons collégiens.
vi, tu as raison. J'écris ces formules surtout pour leur esthétique.
Le contexte ne se veut pas véritablement scolaire.
-
mathelot
 par mathelot » 27 Aoû 2010, 17:16
par mathelot » 27 Aoû 2010, 17:16
mathelot a écrit: \, \left( \frac{ 2^{2010}+1 }{\sqrt{2}} \right) +1})
Bonjour,
calculons la somme sous la racine
+1)
réduisons au même dénominateur
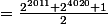
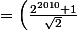^2)
d'où
^2}=\frac{2^{2010}+1}{\sqrt{2}})
-
mathelot
 par mathelot » 29 Aoû 2010, 06:01
par mathelot » 29 Aoû 2010, 06:01
Bonjour,
Simplifier
(2^{2012}-2^{2011}+2^{2010}-2^{2009})}{3}})
Simplifier
 \left( \frac{1}{2^{2011}}+\frac{1}{2^{2010}}+\frac{1}{2^{2009}} \right)})
Simplifier
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)\left( \sqrt{2}+\sqrt{3}-\sqrt{1} \right)\left( \sqrt{1}+\sqrt{3}-\sqrt{2} \right)})
Simplifier
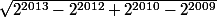
Simplifier

:we:
-
mathelot
 par mathelot » 31 Aoû 2010, 08:15
par mathelot » 31 Aoû 2010, 08:15
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités