Raisonement par recurrence

par **newton** » 17 Juil 2010, 19:24

bonjour j ai un peu de mal sur un exercice

demontrer par recurrence que
n somme k=1 k(k+1)=n(n+1)(n+2)/3 pr n>=1

d habitude ca va mais le k+1 me gene donc j arrive pas a avoir k1 et de continuer

par **Ben314** » 17 Juil 2010, 19:28

Salut,
Si j'ai bien compris, ta somme est :

Ce qui signifie qu'en fait,

et c'est ça qu'il faut utiliser pour faire l'hérédité de ta réccurence.

par **newton** » 17 Juil 2010, 21:06

j avoue que j ai pas compris comment on trouve en premier element 1.2

par **Dinozzo13** » 17 Juil 2010, 22:16

Si

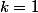
alors

:++:

par **Ben314** » 17 Juil 2010, 22:21

J'ai effectivement, j'ai noté avec un point '.' le produit de 1 par 2...

par **newton** » 18 Juil 2010, 00:10

oui merci je viens de comprendre...
y a plus qu a bien rediger ;)

par **newton** » 18 Juil 2010, 07:57

pour etre sure
donc on trouve bien pour n+1
=(n+1)(n+2)(n+3)/3

par **Ben314** » 18 Juil 2010, 10:17

Oui.
On sait que

donc que

.

On veut montrer (par récurence) que

donc, lorsque l'on fait la partie "héréditée", on suppose que, pour un certain entier n, on a bien

et il faut montrer que la formule est encore vrai au rang suivant, c'est à dire que

par **newton** » 19 Juil 2010, 03:54

je comprend pas bien la on voulait demontrer par recurrence

Sn=n somme k=1 k(k+1)=n(n+1)(n+2)/3
moi je suppose Sn...etc
et S1...=2 donc S1 verifie la propriete

et puis pour n+1 somme k=1 k(k+1)=Sn+(n+1)(n+2)
donc ...

donc quelque soit n E IN* n somme k=1 k(k+1)=n(n+1)(n+2)/3

par **Dinozzo13** » 19 Juil 2010, 07:06

Principe du raisonnement par récurrence :
Soit

un entier naturel et

une propriété définie pour

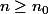
. Si

est vraie pour

et si elle est vrai pour

dès qu'on la suppose vraie pour

, alors,

est vrai pour tout

.

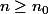
Et là tu te rends compte que ç'est ce qu'a fait Ben314

par **newton** » 19 Juil 2010, 07:22

oui mais si pour n>=1 n0 n est pas !!! non?

par **Ben314** » 19 Juil 2010, 07:55

newton a écrit:oui mais si pour n>=1 n0 n est pas !!! non?

Dans cet exercice, on te demande de montrer une certaine formule pour tout

, c'est à dire que

.

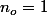
Bon, sinon, ma dernière remarque du post #8 était fausse : je m'était embrouillé les pinceaux : je l'enlève et je modifie le post #8...
désolé.

par **newton** » 19 Juil 2010, 13:29

bon j avais donc reussi l exo
mais merci pour la redefinition du principe de raisonnement par récurrence

par **Carrollsfdgsd** » 19 Juil 2010, 13:53

On m'a expliqué sans que je comprenne que étant une suite arithmétique on avait a+c=2b et étant une suite géométrique on avait a*b=c au carré

On m'a expliqué sans que je comprenne que étant une suite arithmétique on avait a+c=2b et étant une suite géométrique on avait a*b=c au carré

par **Dinozzo13** » 19 Juil 2010, 14:08

newton a écrit:bon j avais donc reussi l exo
mais merci pour la redefinition du principe de raisonnement par récurrence

de rien :++:

Raisonement par recurrence

raisonement par recurrence

sryksryksryksr

Qui est en ligne