Po sur

par **stevi** » 13 Juil 2010, 19:31

salut

je demande est-ce que cette inégalité est juste

9(ab²+bc²+ca²)<= (a+b+c)^3

pour tous réels positifs a et b et c

merci

par **Zweig** » 13 Juil 2010, 19:49

Nope, prends a = b = 1 et c = 0

par **Ben314** » 13 Juil 2010, 20:24

Le mieux que tu puisse obtenir est :

6,75(ab²+bc²+ca²)<= (a+b+c)^3

avec égalité ssi b=2a, c=0 (ou bien c=2b, a=0 ou bien a=2c, b=0)

par **Olympus** » 13 Juil 2010, 22:32

Ben314 a écrit:Le mieux que tu puisse obtenir est :

6,75(ab²+bc²+ca²)<= (a+b+c)^3

avec égalité ssi b=2a, c=0 (ou bien c=2b, a=0 ou bien a=2c, b=0)

Méthode très bourrin : il suffit de constater que

.

Comment j'y suis arrivé ? En jouant avec les cas d'égalité de BenPi, + Wolfram pour m'aider à développer ces gros trucs :ptdr:

par **Olympus** » 13 Juil 2010, 22:39

Et bah non, revérifié mais ma précédente égalité est fausse, enfin, lui manquent des trucs positifs que j'ai la flemme d'ajouter, car sinon, le 144*trucbidule couvre bien toutes les quantités négatives si je ne me trompe pas .

Je vais voir si j'y arrive avec d'autres méthodes moins bourrin, mais ça s'annonce pas facile du tout vu que l'inégalité n'est que cyclique :-/

par **Olympus** » 14 Juil 2010, 13:50

Elle est quand même un peu dure je trouve ...

Enfin, y a plus fort :

( dans ce cas, le cas d'égalité est a=b=c, ou a=2b ET c=0 ( + ses permutations cycliques ) ) .

En supposant que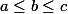

, l'inégalité devient quasiment triviale avec AM-GM . Mais c'est justement là le problème, je ne pense pas que cette supposition soit légitime vu que l'inégalité n'est pas symétrique ...

Des pistes ?

Pour l'instant je regarde ce que ça donne si je mets tout au degré 4 ( en multipliant par (a+b+c) ) .

Po sur

po sur

Qui est en ligne