Famille libre indénombrable.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 05 Juil 2010, 21:12
par Doraki » 05 Juil 2010, 21:12
On admet que e est transcendant.
1) Montrez qu'il existe une séquence d'entiers (an) telle que toute combinaison linéaire infinie à coefficients entiers, bornés, et non tous nuls, de {e^-an} est non nulle
2) Montrez qu'il existe un ensemble X de parties infinies de N, indénombrable, tel que pour tous I,J de X, l'intersection de I et J est finie.
3) En déduire que la famille indénombrable
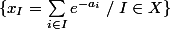
est libre sur Q.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Juil 2010, 22:16
par ffpower » 05 Juil 2010, 22:16
Question con mais je préfère être sur pour pas partir sur du HS :
Libre=Libre sur Q?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Juil 2010, 22:25
par Ben314 » 05 Juil 2010, 22:25
Je comprend pas trop l'énoncé :
Vu la définition des
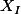
, n'a t'on pas forcément
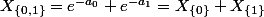
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Juil 2010, 08:49
par Doraki » 06 Juil 2010, 08:49
Ah oui tiens comment j'ai pu ne pas m'en rendre compte.
C'est pas grave il faut juste une autre petite question intermédiaire.
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 06 Juil 2010, 10:32
par windows7 » 06 Juil 2010, 10:32
on doit avoir an -> +infini
on remarque aussi que pour tout k dans IN on ne peut pas avoir an = o(n^k)
ce qui permet de penser a un certain an :zen:
tu m'as deja posé la 2) en privé donc je ne vais pas tricher ..

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Juil 2010, 07:19
par Ben314 » 07 Juil 2010, 07:19
Pour la question 1), les coeff. des "combinaisons linéaires infinie", clairement, ils sont pas dans R (sinon, ça marche pas) mais ils sont dans Z (cas dans lequel j'entrevois une méthode) ou dans Q (cas dans lequel j'entrevois pas gras...) ?
Pour la 2), je propose d'associer à tout réel
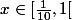
l'ensemble
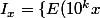\, ,\, k\in{\bb N}^*\})
(où
)
désigne la partie entière de

)
Il est clair que
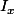
est infini et que, si
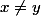
alors
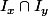
est fini.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Juil 2010, 07:53
par Doraki » 07 Juil 2010, 07:53
Ils sont dans Z, pardon.
Dans R ça marche clairement pas, et dans Q..., avec un nombre fini de coefficients distincts, c'est la même chose que dans Z, mais avec une infinité de coefficients distincts, je sais pas.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Juil 2010, 08:57
par Ben314 » 07 Juil 2010, 08:57
Dans ce cas, pour le 1), je verrais bien une construction par recurrence :
On prend par exemple
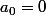
puis, pour

, si
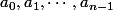
sont construit, on considère le minimum

des
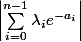
lorsque
)
décrit l'ensemble
fini ^{n})
privé de
)
.
Comme
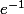
est trancendant,
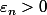
et on peut donc choisir un
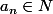
tel que
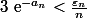
.
Sauf erreur, ça marche...
La déduction du 3) est alors assez évidente...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Juil 2010, 09:20
par Doraki » 07 Juil 2010, 09:20
je suis pas sûr que e^-an < en/n soit une contrainte suffisante, vu que le produit des (1-1/n) tend vers 0.
Sinon le reste marche bien, et oui le 3 est là juste pour la conclusion.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Juil 2010, 10:40
par Ben314 » 07 Juil 2010, 10:40
Bon, esssayons de rédiger...
On a
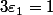
et
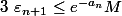
tels que
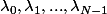
soient non tous nuls.
Sauf erreur,
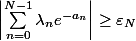
par définition de
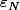
et, comme
...(N+1)N}\ <br /><\ M\varepsilon_N\sum_{k\geq 1}\frac{1}{N^k}\ <br />=\ \frac{M\varepsilon_N}{N-1}\ <br />\leq \varepsilon_N)
On en déduit que
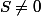
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
