Produit scalaire(théorie)

[bacha]

salut
je voulais démontrer la théorie suivante :
"soit u,v,w des vecteurs :u.(v+w)=u.v+u.w"

pour la démontrer j'ai fais:
u.(v+w)=1/2(llu+v+wll^2-llull^2-llv+wll^2)...•
u.v+u.w=(1/2(llu+vll^2-llull^2-llvll^2))+(1/2(llu+wll^2-llull^2-llvll^2)...••
de• et•• en trouve:
[1/2(llu+v+wll^2-llull^2-llv+wll^2)]-[(1/2(llu+vll^2-llull^2-llvll^2))+(1/2(llu+wll^2-llull^2-llvll^2)]=....
mais le résultat n'était pas 0 ,donc je trouve que cette méthode de démonstration n'est pas juste et.
svp aidez moi a trouver la bon méthode !

[girdav]

Bonjour,
si je comprends bien on doit montrer la linéarité à droite du produit scalaire à l'aide de la définition .
On voit en remplaçant par que ce qui permet de voir sans utiliser la linéarité que l'on doit démontrer (ce qui est quand même la moindre des choses) que .

Ça devrait t'aider dans ton développement.

[bacha]

Bonjour,
si je comprends bien on doit montrer la linéarité à droite du produit scalaire à l'aide de la définition .
On voit en remplaçant par que ce qui permet de voir sans utiliser la linéarité que l'on doit démontrer (ce qui est quand même la moindre des choses) que .

Ça devrait t'aider dans ton développement.

merci pour votre réponse

[greg78]

en même temps, je ne vois pas bien le sens d'une telle démonstration. Le produit scalaire est par définition une forme bilinéaire, symétrique, définie positive. Donc la linéarité à droite, à gauche, et pour chacune des variables n'est pas une propriété mais bien une définition...

Et pour le démontrer, on va au contraire chercher des propriétés, qui pour être utilisable doivent bien avoir été démontrée à un moment ou l'autre, et utilisent elles mêmes la bilinéarité. Enfin bref, on tourne un peu en rond.

[benekire2]

Faut il encore démontrer que le produit scalaire est un produit scalaire :id:

Bon après ces définitions sont pas celles que j'aurais prisent car on voit bien qu'elles viennent d'ailleurs ... J'aurais prit u.v=||u||*||v||*cos(u,v)

Bon après on va me dire que on défini souvent le cosinus d'un réel comme quotient de u.v et du produit des normes des deux vecteurs ... :mur:

[greg78]

C'est d'ailleurs peut-être ce qu'il voulait faire, vérifier que le produit scalaire canonique de est bien un produit scalaire.

A ce moment là, le plus simple est de se placer dans une base orthonormée et de considérer l'application f : avec u=(x,y) et v=(x',y').

Là on peut bien vérifier que c'est bilinéaire, symétrique, et défini positif. Donc le produit scalaire est un produit scalaire ! On est sauvé...

[bacha]

C'est d'ailleurs peut-être ce qu'il voulait faire, vérifier que le produit scalaire canonique de est bien un produit scalaire.

A ce moment là, le plus simple est de se placer dans une base orthonormée et de considérer l'application f : avec u=(x,y) et v=(x',y').

Là on peut bien vérifier que c'est bilinéaire, symétrique, et défini positif. Donc le produit scalaire est un produit scalaire ! On est sauvé...

merci, je pouvais travailler analytiquement ,mais je voulais travaillé avec l'autre théorie comme vous avez vu ,c'est facile en utilisant x et y ,donc je voulais bien rentrer dons la zone difficile en travaillant avec les vecteurs .

[benekire2]

C'est moins facile mais passible de démontrer que ||u||*||v||*cos(u,v) est un produit scalaire évidemment. Ca doit se trouver sur internet, ou en tapant "produit scalaire" dans une recherche sur ce forum. Trouve le topic de Qmath.

[girdav]

En fait ce que je proposais, c'est à partir de la définition de 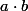par , montrer que ceci définit bien un produit scalaire, en utilisant le fait que est une norme (d'ailleurs non nécessairement euclidienne). Ça permet d'obtenir que (par positive homogénéité) et de poursuivre le développement tenté lors du premier message de la discussion.
Tout se simplifie bien par la formule qui s'établit uniquement avec la définition.

[ffpower]

sauf que c'est faux. Pour que ca définisse produit scalaire, il faut que l'on ait l'identité du parallélogramme ||u+v||²+||u-v||²=2(||u||²+||v||²) ( c'est une CNS )
Donc pour pouvoir conclure avec cette définition, il faudra nécessairement à un moment ou un autre utiliser une propriété de la norme euclidienne autre que les 3 axiomes de définition des normes. Après ca peut être l'identité du parallélogramme ( sauf que c'est pas sur qu'elle soit évidente à prouver sans utiliser le produit scalaire, mais bon, p-e qu'il existe une preuve géométrique ), ou l'expression cartésienne de la norme, ou autre chose, mais en tout cas faudra utiliser un truc.

[Le_chat]

En fait ce que je proposais, c'est à partir de la définition de par ,

Un peu douteux comme définition...

[girdav]

Un peu douteux comme définition...

C'est ce que l'on comprend du premier message. Si vous avez compris autre chose, prière de me le signaler afin de ne pas me laisser dans l'erreur.

[Le_chat]

je voulais dire que la formule n'est pas bonne!

[ffpower]

comment ca? c'est la formule de polarisation classique non?

[bacha]

je ne comprend vraiment pas ce que vous dites ,donc svp donnez moi juste une explication

[greg78]

Le truc, c'est que si on reprend ta question d'origine, pour peu que je la comprenne bien, tu cherches à démontrer que :
"soit u,v,w des vecteurs :u.(v+w)=u.v+u.w".

Autrement dit tu souhaite montrer la linéarité (à droite en l'occurence) du produit scalaire. Mais, comme je l'ai déjà dit plus tôt, il n'y a pas de démonstration à faire car ce n'est pas une propriété d'un produit scalaire mais bien une partie de sa définition. Encore une fois, on défini le produit scalaire comme une forme (ie d'un espace vectoriel à valeur dans ou ) bilinéaire (ie par rapport à chacune des deux variables), symétrique et définie positive.
Donc si ton application est un produit scalaire, la linéarité sera acquise. En revanche, pour montrer qu'une application est un produit scalaire, alors là tu verifieras sa bilinéarité. Mais il faut en avoir une expression analytique.

Typiquement on peut citer comme produit scalaire , ou aussi .

Après, le produit scalaire vérifie plusieurs identités, les identités de polarisation, qui ont été évoquées dans la discussion.
Ainsi,

et .
Cependant d'autres application bilinéaires symétriques peuvent vérifier ces relations. Pour que ce soit un produit scalaire, il vaut que la norme soit euclidienne, c'est a dire qu'on ait un produit scalaire tel que .
On peut risquer ici de tourner en rond mais il existe une CNS pour qu'une norme soit euclidienne, qui est de vérifier l'identité du parallélogramme, ie la troisième identité de polarisation.

Avec tout cela, connaissant une norme (qu'on suppose euclidienne ici), tu peux déterminer son produit scalaire !

J'espère avoir un tant soit peu répondu à ta question ou tout au moins éclairci certaines chose sur le produit scalaire.

[ft73]

je ne comprend vraiment pas ce que vous dites ,donc svp donnez moi juste une explication

Cette propriété * se démontre par exemple en utilisant l'expression du produit scalaire en repère orthonormé.

* tu es en quelle classe Bacha ? si tu es <= terminale, tu es tout à fait ok avec les programmes et leur déf. du produit scalaire

[girdav]

désigne la norme euclidienne.
Je ne l'avais pas réalisé sur le coup mais c'était implicitement supposé, car je ne pense pas que l'on introduise d'autres normes au lycée.
Évidemment, le résultat est faux pour une norme quelconque. Par exemple, sur , en posant et avec la "définition" (), on a et donc pas de "linéarité à droite" qui tienne.

[ft73]

désigne la norme euclidienne.
Je ne l'avais pas réalisé sur le coup mais c'était implicitement supposé, car je ne pense pas que l'on introduise d'autres normes au lycée.
Évidemment, le résultat est faux pour une norme quelconque. Par exemple, sur , en posant et avec la "définition" (), on a et donc pas de "linéarité à droite" qui tienne.

Il est évident que la norme euclidienne est la seule enseignée au lycée. Ce point d'entrée du produit scalaire est quand même assez naturel, et en effet on polarise cette norme, qu'on n'a surtout pas présentée comme une forme quadratique ^^

[ffpower]

Après si on sait que c'est précisément la norme euclidienne classique ( ), bah le plus simple je pense c'est de vérifier alors que . Mais vu que ca c'est une autre définition du produit scalaire, c'est bizarre que l'exo veuille qu'on parte de la définition du produit scalaire par les normes. Bref, exo louche moi je dis