Matrice - Application aux suites
23 messages
- Page 1 sur 2 - 1, 2
Matrice - Application aux suites
Bonjour,
J'ai un système de suites définies pas:
Un+1 = -7Un - 6vn
Vn+1 = 12Un + 10 Vn
1. Je dois transformer ce système sous forme matricielle, diagonaliser la matrice, Calculer An et en déduire Un et Vn
La matrice diagonale est
2 0
0 1
A^n =
-7^n -6^n
12^n 10^n
Donc Un = An* U0
Par contre la ou j'ai du mal c'est quand on demande pour qu'elles valeurs (U0, V0) les suites Un et Vn sont convergentes... ?
je dois ensuite calculer la lim en l'infini de ( U²n+1 + V²n+1 ) / ( U²n + V²n ) en utilisant les équivalences...
:cry:
Merci d'avance !
J'ai un système de suites définies pas:
Un+1 = -7Un - 6vn
Vn+1 = 12Un + 10 Vn
1. Je dois transformer ce système sous forme matricielle, diagonaliser la matrice, Calculer An et en déduire Un et Vn
La matrice diagonale est
2 0
0 1
A^n =
-7^n -6^n
12^n 10^n
Donc Un = An* U0
Par contre la ou j'ai du mal c'est quand on demande pour qu'elles valeurs (U0, V0) les suites Un et Vn sont convergentes... ?
je dois ensuite calculer la lim en l'infini de ( U²n+1 + V²n+1 ) / ( U²n + V²n ) en utilisant les équivalences...
:cry:
Merci d'avance !
Salut,
Je comprend franchement pas ce que tu as fait...
"Transformer ce système sous forme matricielle", c'est tout simplement écrire le système sous la forme :
=<br />\left(\matrix{?& ?\cr ? & ?}\right)<br />\left(\matrix{U_{n}\cr V_{n}}\right)) ce qui ne demande absolument aucun calculs.
ce qui ne demande absolument aucun calculs.
On en déduit par réccurence que, pour tout entier , on a
, on a =A^n\left(\matrix{U_{o}\cr V_{o}}\right)) où
où  est la fameuse matrice
est la fameuse matrice ) .
.
Enfin, si) alors
alors 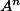 n'est absolument pas du tout égal à
n'est absolument pas du tout égal à ) !!!!
!!!!
C'est là qu'il faut diagonaliser (i.e. écrire
(i.e. écrire 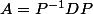 avec
avec  diagonale)pour pouvoir évaluer simplement
diagonale)pour pouvoir évaluer simplement 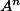 ...
...
Je comprend franchement pas ce que tu as fait...
"Transformer ce système sous forme matricielle", c'est tout simplement écrire le système sous la forme :
On en déduit par réccurence que, pour tout entier
Enfin, si
C'est là qu'il faut diagonaliser
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Julien57160 a écrit:Donc voila pour Un et Vn.
Un = -8.2n+9 -6.2n-9 U0
Vn = 12.2n-12 9.2n-8 V0
T'as un -9 à la place d'un +6
Normalement on a
Un = (-8*2^n+9)*U0 + (-6*2^n+6)*V0
Vn = (12*2^n-12)*U0 + (9*2^n-8)*V0.
(tu peux vérifier en prenant n=0 et n=1 qu'on a les bonnes relations).
Pour le reste y'a des moyens plus ou moins faciles de trouver quand (Un,Vn) converge.
On peut toujours expérimenter :
Si on prend au hasard U0 = V0 = 1, que valent Un et Vn en fonction de n et est-ce que ça converge ?
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
