Fonction analytique
17 messages
- Page 1 sur 1
fonction analytique
Bonjour,
A t-on: Une fonction est analytique ssi pour tout x0 il existe un voisinage de x0 tel que f(x) est égale au developpement en série de taylor en x0
?
A t-on: Une fonction est analytique ssi pour tout x0 il existe un voisinage de x0 tel que f(x) est égale au developpement en série de taylor en x0
?
Salut,
La fonction que tu cherche correspond au problème classique du "recollement C^oo".
Pour ton cas particulier, tu part de la fonction f définie sur R par :
=\left\{\matrix {\exp\big(\frac{1}{x(x-1)}\big)&{\rm si } x\in]0,1[\cr<br />0\ \ \ \ \ \ &{\rm sinon }}\right.)
On vérifie facilement que g est C^oo sur R (avec g(0)=g(1)=0)
Tu n'as alors plus qu'à considérer=\frac{1}{\lambda}\int_{-\infty}^xg(t)\, dt) où
où 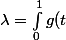\, dt) ...
...
La fonction que tu cherche correspond au problème classique du "recollement C^oo".
Pour ton cas particulier, tu part de la fonction f définie sur R par :
On vérifie facilement que g est C^oo sur R (avec g(0)=g(1)=0)
Tu n'as alors plus qu'à considérer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Donc les fonctions proposées ne corespondent pas..
Je n'ai jamais dit que la mienne fonctionnait, mais qu'on pouvait construire la tienne à partir de celle que je propose ...
une telle fonction est elle forcement de cette "forme"?(l'integrale de l'exponentielle d'inverse)?
Non, bien sur que non, il y en a une infinités d'autres. Mais c'est cette forme qu'on prend en général.
Si tu as une fonction f C^oo dont toutes les dérivées sont nulles en 0 et qui pourtant est non nulle au voisinage de 0, c'est qu'elle croit extrèmement lentement (plus lentement que tout x->x^n).
Si on pose g(x)=1/f(1/x) cela signifie que g tend extrèmement rapidement vers +oo lorsque x->oo (plus vite que tout x->x^n).
Existe t-il beaucoup de telles fonctions ? Ben oui, il y en a une ENOOOORME infinité. Par contre parmi la petite dixaine de fonction dites "usuelles", ben grosso modo il y a que l'exponentielle qui vérifie ça.
Aprés, si tu préfère, tu peut prendre le cosinus ou le sinus hyperbolique ou bien la fonction x->x^x voire la fonction (x^x)^x comme fonction g qui tend trés vite vers l'infini quand x->oo.
Tu pose alors f(x)=1/g(1/x) pour x>0 et f(x)=0 pour x=<0 et tu as une fonction C^oo mais pas analytique en 0.
Si on pose g(x)=1/f(1/x) cela signifie que g tend extrèmement rapidement vers +oo lorsque x->oo (plus vite que tout x->x^n).
Existe t-il beaucoup de telles fonctions ? Ben oui, il y en a une ENOOOORME infinité. Par contre parmi la petite dixaine de fonction dites "usuelles", ben grosso modo il y a que l'exponentielle qui vérifie ça.
Aprés, si tu préfère, tu peut prendre le cosinus ou le sinus hyperbolique ou bien la fonction x->x^x voire la fonction (x^x)^x comme fonction g qui tend trés vite vers l'infini quand x->oo.
Tu pose alors f(x)=1/g(1/x) pour x>0 et f(x)=0 pour x=<0 et tu as une fonction C^oo mais pas analytique en 0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Non, ce ne sont pas les seules, il y en a une infinité, une ENORME infinité comme le dit si bien Ben314. Et c'est aisément imaginable, on voit très bien en imaginant le graphe d'une telle fonction qu'il y a une infinité de possibilités.
Le seul problème, c'est que trouver une formule explicite est plus délicat.
On doit certainement trouver, en cherchant loin, une formule qui n'utilise pas d'exponentielle, ni de près, ni de loin, mais c'est pas tellement intéressant.
Le seul problème, c'est que trouver une formule explicite est plus délicat.
On doit certainement trouver, en cherchant loin, une formule qui n'utilise pas d'exponentielle, ni de près, ni de loin, mais c'est pas tellement intéressant.
bonjour,
les fonctions réelles que nous évoquons:

avec tous les nombres dérivés nuls en un point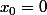 ,
,
qui ne sont pas somme de leur série de Taylor,
style
ont des applications en "distributions",
elles servent à construire des "partitions de l'unité"
c'est une somme , localement finie, sur un ensemble d'indices I qui peut être
non dénombrable, de fonctions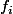 à support compact
à support compact
telle que
=1)
ces partitions servent à rendre une construction dans "locale"
"locale"
les fonctions réelles que nous évoquons:
avec tous les nombres dérivés nuls en un point
qui ne sont pas somme de leur série de Taylor,
style
ont des applications en "distributions",
elles servent à construire des "partitions de l'unité"
c'est une somme , localement finie, sur un ensemble d'indices I qui peut être
non dénombrable, de fonctions
telle que
ces partitions servent à rendre une construction dans
Les partitions de l'unité ont aussi pas mal d'applications en géométrie différentielle, en topologie, en analyse, ...
Les fonctions de ce style servent aussi à construire des noyaux régularisants pour la convolution.
Bref, tout ça n'est pas juste une petite amusette sur des fonctions biscornues, mais a de réelles applications.
Les fonctions de ce style servent aussi à construire des noyaux régularisants pour la convolution.
Bref, tout ça n'est pas juste une petite amusette sur des fonctions biscornues, mais a de réelles applications.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
