Demande énoncé 1ereS
14 messages
- Page 1 sur 1
demande énoncé 1ereS
Bonjour à tous !
j'aurai besoin d'un énoncé de DS ("devoir surveillé") de niveau
fin d'année de 1èreS.
De préférence complet (fonctions,dérivées,limites,etc.) et
de difficulté moyen-dûr.
merci d'avance.
j'aurai besoin d'un énoncé de DS ("devoir surveillé") de niveau
fin d'année de 1èreS.
De préférence complet (fonctions,dérivées,limites,etc.) et
de difficulté moyen-dûr.
merci d'avance.
Voici quelques propositions :
[url="http://www.hebergementimages.com/image-72fc891876b0234a5d51ecdcb140cb5d_Sans-titre.jpg.html"] [/url]
[/url]
Lien sponsorisé : [url="http://www.hebergementimages.com/"]hebergement image[/url]
[url="http://www.hebergementimages.com/image-0ed9776c7c8c5585d2906ceb76f1cb93_Sans-titre.jpg.html"] [/url]
[/url]
Lien sponsorisé : [url="http://www.reductionet.com/code-reduction-code-chouchou-3suisses-353.html"]code promo 3 suisses[/url]
voilà
[url="http://www.hebergementimages.com/image-72fc891876b0234a5d51ecdcb140cb5d_Sans-titre.jpg.html"]
 [/url]
[/url]Lien sponsorisé : [url="http://www.hebergementimages.com/"]hebergement image[/url]
[url="http://www.hebergementimages.com/image-0ed9776c7c8c5585d2906ceb76f1cb93_Sans-titre.jpg.html"]
 [/url]
[/url]Lien sponsorisé : [url="http://www.reductionet.com/code-reduction-code-chouchou-3suisses-353.html"]code promo 3 suisses[/url]
voilà
Après tout dépend le niveau que l'on veut, mais je pensais a un exo du genre où il faut trouver toutes les fonctions telles qu'elles aient "un point fixe sous la normale" on doit introduire les primitives pour résoudre une équation différentielle . Bien sûr le mieux si tu veut être synthétique c'est une bête étude de fonction type bac. C'est relativement complet pour asymptotes/dérivée/fonctions/polynômes après il faut faire un exo de suites , et un autre orienté produit scalaire+barycentres+relations métriques ( en gros étude d'une configuration + des lieux de points qui utilisent th de la médiane, barycentres , carrés scalaires ...
Salut,
Tu peux jeter un coup d'il sur notre DS ( c'est pas un DS de fin d'année mais bon ) sur les fonctions ( dérivées, limites etc... ) : http://maths-forum.com/showthread.php?t=102335 . Tu peux ignorer le 5ème exercice qui traite des transformations, mais ce n'est qu'un exercice d'application ( pas besoin de réfléchir en gros ) .
Tu peux jeter un coup d'il sur notre DS ( c'est pas un DS de fin d'année mais bon ) sur les fonctions ( dérivées, limites etc... ) : http://maths-forum.com/showthread.php?t=102335 . Tu peux ignorer le 5ème exercice qui traite des transformations, mais ce n'est qu'un exercice d'application ( pas besoin de réfléchir en gros ) .
Salut !
Je te propose des exos tirés de mes DS et de mes compositions.
I : Soit la fonction définie par :
définie par : =-4x^3+3x-\frac{1}{2}) .
.
On admet quel'équation=0) admet trois solutions dans l'intervalle
admet trois solutions dans l'intervalle  .
.
1°) Déterminer les solutions dans de l'équation :
de l'équation : =\frac{1}{2}) .
.
Représenter ces solutions sur le cercle trigonométrique.
2°) Démontrer que :=3\sin(a)-4(\sin(a))^3) .
.
En déduire les solutions de=0) .
.
II : Soit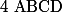 un rectangle de centre
un rectangle de centre 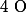 tel que, en centimètre :
tel que, en centimètre : 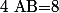 et
et 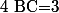 .
.
1°)a) Construire le point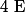 tel que :
tel que : 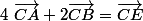 .
.
b) Déterminer l'ensemble des points
des points  du plan tels que :
du plan tels que :
. \vec{MD}=0)
2°) Déterminer l'ensemble des points
des points  du plan tels que :
du plan tels que :
. \( \vec{MA}+\vec{MC} \)=0)
3°) Déterminer l'ensemble des points
des points  du plan tels que :
du plan tels que :
.\( \vec{MA}+2\vec{MB}+\vec{MC} \)=0)
III : Etudier la fonction définie par :
définie par : =\frac{3x^4-5x^2+2}{|x+3|+|x-3|})
(Domaine, parité éventuelle, limites aux bornes de f,dérivée, variations)
IV : Résoudre dans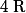 :
:
1°)\cos x + \sqrt 2=0)
2°)
V : Démontrer que quelque soit l'entier naturel ,
,  est divisible par
est divisible par 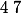 .
.
VI : Les fonctions et
et  sont définies par :
sont définies par :
=\sqrt{x-4}) et
et =\frac{-3x^2+8x}{x-1})
1°) Déterminer et
et 
2°) Calculer) et
et ) .
.
Déterminer et
et 
3°) Déterminer la parité éventuelle de et
et  .
.
4°) Calculer les coordonnées des points d'intersection des courbes C et C' représentatives respectivement de et
et 
5°) Etudier les positions relatives des courbes C et C'
Bon travail :++:
Je te propose des exos tirés de mes DS et de mes compositions.
I : Soit la fonction
On admet quel'équation
1°) Déterminer les solutions dans
Représenter ces solutions sur le cercle trigonométrique.
2°) Démontrer que :
En déduire les solutions de
II : Soit
1°)a) Construire le point
b) Déterminer l'ensemble
2°) Déterminer l'ensemble
3°) Déterminer l'ensemble
III : Etudier la fonction
(Domaine, parité éventuelle, limites aux bornes de f,dérivée, variations)
IV : Résoudre dans
1°)
2°)
V : Démontrer que quelque soit l'entier naturel
VI : Les fonctions
1°) Déterminer
2°) Calculer
Déterminer
3°) Déterminer la parité éventuelle de
4°) Calculer les coordonnées des points d'intersection des courbes C et C' représentatives respectivement de
5°) Etudier les positions relatives des courbes C et C'
Bon travail :++:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
