Etude de fonction (exercice)

[adel01]

bien le salut a vous .......
voila je voudrais que quelqu'un m'explique ce que veut dire le minimum pour une fonction .......... comme vous pouvez le voir sur la solution de cet exercie ... :we:
et ma deuxieme question concernera l'ensemble de solution que je n'arrive pas a comprendre ...... :triste:

[Mathusalem]

bien le salut a vous .......
voila je voudrais que quelqu'un m'explique ce que veut dire le minimum pour une fonction .......... comme vous pouvez le voir sur la solution de cet exercie ... :we:
et ma deuxieme question concernera l'ensemble de solution que je n'arrive pas a comprendre ...... :triste:

Ton tableau te dit que tu décrois de sur l'intervalle ]-inf,2[ et que tu crois sur l'intervalle ]2,+inf[
Si tu fais un dessin, ça veut dire que le point où t'arrêtes de décroître et où tu commences à croître est le point le "plus bas possible" sur le graphe. C'est donc ton minimum. Il n'existe pas de valeurs plus petites que ton minimum pour cette fonction. En gros, ça veut dire que ta fonction fait un sourire, dont la pointe touche la valeur 1.
Et donc forcément par définition du minimum, pour n'importe quel x, f(x) ou = à 1. (donc tu peux prendre tout x dans R)

Si tu veux vraiment te convaincre plus que ça, dessine la courbe f(x) = x^2 + 1.C'est la courbe que tu étudies.

[gigamesh]

Si tu veux vraiment te convaincre plus que ça, dessine la courbe f(x) = x^2 + 1.C'est la courbe que tu étudies.

plutôt

[busard_des_roseaux]

Bj,

les minima se détectent avec le tableau de variation


il faut bien distinguer entre minimum local et minimum global

def
le minimum global est la plus petite des images de f.


exemple 1

1 est minimum global de f pour
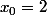
il est atteint en et

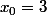exemple 2
1 est minimum global de

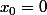
il est atteint en au bord du domaine de définition.
la dérivée ne s'annule pas.


def
on parle de minimum local
si

i) on peut trouver un intervalle ouvert

inclu dans le domaine
de définition
ii) est minimum sur l'intervalle I

exemple 3
primitive de
admet un minimum local en
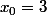
comme on le voit en dessinant le tableau de variation
ce minimum n'est pas global


prop1
en un minimum local, la dérivée s'annule

prop2
La dérivée s'annule en un minimum global ,atteint en un point
non situé sur le bord du domaine de définition.

[adel01]

donc on aura quelque chose comme ca ?

[busard_des_roseaux]

1 est minimum global de la fonction atteint en

il faut translater ta courbe de vers la droite
le minimum est atteint en

[adel01]

1 est minimum global de la fonction atteint en

il faut translater ta courbe de vers la droite
le minimum est atteint en

non je pense que tu te trempe le minimum est atteint en f(0) = 1 :we: si on a

[busard_des_roseaux]

non je pense que tu te trompes, le minimum est atteint en f(0) = 1 :we: si on a

re,

dans une fonction, il y a un ensemble de départ , içi R, et un ensemble
d'arrivée, R aussi.

f(0) se calcule en remplaçant x par zéro

[adel01]

donc on aurra 1 en f(2) c ca ? :zen: