Concours Audioprothésiste Paris (Intégrale et étude fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 14:45
par jacky.C » 19 Juin 2010, 14:45
Bonjour, j'ai passé les concours d'audioprothésiste à Paris.
Voici une partie du sujet, pouvez vous me donner une succincte correction de ces deux exercices svp, ce serait très gentil


MERCI !
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 19 Juin 2010, 15:06
par windows7 » 19 Juin 2010, 15:06
tu sais faire quoi ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 19 Juin 2010, 15:15
par Arnaud-29-31 » 19 Juin 2010, 15:15
Bonjour,
Le premier exo (qui même si c'est compréhensible a un énoncé que je trouve vraiment limite ^^) nous amène tout d'abord à trouver une primitive de
.e^{2x-1})
On peut d'abord chercher une primitive de

qui tout calcul fait donne
)
On ne garde ensuite que la partie imaginaire ce qui nous donne une primitive de la forme
 - n.cos(nx)))
Ensuite pour l'intégrale de 0 à

, on évalue cette primitive en

et en zéro.
Cela donne
.e^{2\pi-1} + \frac{n}{e}))
)
peut aussi s'écrire
^n)
... il ne reste plus qu'à distinguer les cas n pair et n impair.
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 15:17
par jacky.C » 19 Juin 2010, 15:17
:)
Alors dans le premier exercice le souci est que je n'arrive pas à exprimer In en fonction de x et de n, j'ai essayer de faire une double intégration par parties mais j'aboutis un un résultat encore plus compliqué ...
Et pour l'exercice 2, je ne sais pas si il faut à chaque fois faire pour m < 0 et m>0 ?
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 19 Juin 2010, 15:17
par windows7 » 19 Juin 2010, 15:17
je suis pas bien sur que cest la methode qu'il attend ..
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 19 Juin 2010, 15:18
par windows7 » 19 Juin 2010, 15:18
oui faut traiter les deux cas
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 15:24
par jacky.C » 19 Juin 2010, 15:24
Merci Arnaud pour ta réponse, mais les primitives de
Arnaud-29-31 a écrit:
ne sont pas de mon (faible) niveau :we: ... N'y a t-il pas un moyen simplement avec une intégration par parties ?
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 15:26
par jacky.C » 19 Juin 2010, 15:26
Merci Windows7, je vais essayer de faire cas par cas alors mais bon c'est répétitif ...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 19 Juin 2010, 15:27
par Arnaud-29-31 » 19 Juin 2010, 15:27
?? l'exponentiel complexe est au programme de terminale, j'ai du mal à croire que la méthode soit inadaptée ...
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 15:43
par jacky.C » 19 Juin 2010, 15:43
Hum si c'est au programme, mais le raisonnement que tu as fais m'est inconnu ... je ne comprend pas bien. Je vais regarder ça de plus près. merci
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 19 Juin 2010, 15:44
par Arnaud-29-31 » 19 Juin 2010, 15:44
La double intégration par partie n'est pas plus lourde et marche très bien ... Tu peux rester la dessus.
Je te donne les lignes essentielles :
}_{u}.\underbrace{e^{2x-1}}_{v'}.dx \hspace{35}\begin{Bmatrix} u = sin(nx) \hspace{10} u' = n.cos(nx) \\ v' = e^{2x-1} \hspace{10} v = \frac12.e^{2x-1} \end{Bmatrix})
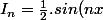.e^{2x-1} - \frac{n}{2}.\int \underbrace{cos(nx)}_{u}.\underbrace{e^{2x-1}}_{v'}.dx \hspace{35}\begin{Bmatrix} u = cos(nx) \hspace{10} u' = -n.sin(nx) \\ v' = e^{2x-1} \hspace{10} v = \frac12.e^{2x-1} \end{Bmatrix})
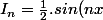.e^{2x-1} - \frac{n}{2}.\left(\frac12.cos(nx).e^{2x-1} + \frac{n}{2}.\underbrace{\int sin(nx).e^{2x-1}.dx}_{I_n}\right))
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 16:12
par jacky.C » 19 Juin 2010, 16:12
Ha très bien ! merci de la réponse. je vais regarder tout de suite ;)
-
jacky.C
- Membre Naturel
- Messages: 26
- Enregistré le: 09 Sep 2009, 15:00
-
 par jacky.C » 19 Juin 2010, 16:31
par jacky.C » 19 Juin 2010, 16:31
Je voulais savoir aussi, est-ce que vous avez une méthode pour savoir quelle fonction vaut mieux dériver et ou primitiver quand on fait une intégration par parties ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 19 Juin 2010, 17:41
par Arnaud-29-31 » 19 Juin 2010, 17:41
Non, ça c'est un petit peu à la louche ... On choisit d'intégrer ce que l'on sait intégrer et on dérive le reste. Ici on aurait pu faire autrement vu qu'on sait intégrer sin(nx) et cos(nx).
-
vingtdieux
- Membre Relatif
- Messages: 196
- Enregistré le: 27 Mai 2010, 22:22
-
 par vingtdieux » 19 Juin 2010, 21:46
par vingtdieux » 19 Juin 2010, 21:46
On arrive à la même chose en intégrant deux fois par parties. En effet sin (nx) passe a ncos(nx) qui reviendra n^2sin(nx), l'expo ne changeant que du facteur 1/2 on a encore la meme integrale. Ala fin:
I (1+(n^2)/4)= 1/2 (sin(nx)-n/2cos(nx))e^(2x-1)+Cte
:doh: Je n'avais pas vu la seconde page des reponses.....
 par busard_des_roseaux » 20 Juin 2010, 06:15
par busard_des_roseaux » 20 Juin 2010, 06:15
jacky.C a écrit:Je voulais savoir aussi, est-ce que vous avez une méthode pour savoir quelle fonction vaut mieux dériver et ou primitiver quand on fait une intégration par parties ?
Bj,
Il vaut mieux primitiver sin(nx) en
 \over n})
ce qui facilite une étude de limite quand
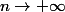
 par busard_des_roseaux » 20 Juin 2010, 06:30
par busard_des_roseaux » 20 Juin 2010, 06:30
Bj,
Pour l'exo (3)
i)
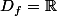
f est continue et dérivable sur R
pour les limites, étudier log(f) puis revenir à f.
ii)
si m>0
=+\infty)
=+\infty)
si m0 ou m<0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités

