Application de l'homogénéisation

par **Ben314** » 16 Juin 2010, 15:06

Olympus a écrit:@poiuytreza : Euh je ne parle pas non plus des bases de la géométrie des complexes enseignées en TS, mais plutôt des techniques présentées dans les livres cités ici http://www.artofproblemsolving.com/Forum/viewtopic.php?f=50&t=20205, comme "Complex Numbers from A to Z" de Titu Andreescu et Dorin Andrica .

Allez, tient, juste pour voir, torche moi avec des complexes et toute la "géométrie invertive" (que je sais pas ce que c'est) que tu veut le petit problème suivant :
Soient C le cercle circonscrit à un triangle (non dégénéré) et C' son cercle inscrit.
Partant d'un point M de C, on construit les deux tangentes T1 et T2 à C'passant par M.
Ces deux tangentes recoupent C respectivement en N1 et N2.
Montrer que la droite (N1N2) est tangente à C'...

Juste pour dire que NON, la géométrie, contrairement aux inégalités, ça ne se résume pas et ça ne se résumera jamais à deux/trois recettes que l'on applique.

par **Olympus** » 16 Juin 2010, 15:17

Je n'ai pas non plus dit que je maîtrise la géo :hein: ( je n'ai même pas fini avec les inégalités ), mais la plupart des problèmes que j'ai vu sur le forum de AOPS avaient des solutions avec les complexes . D'ailleurs, dans le livre de Titu, les problèmes d'IMO sont même catégoriés dans le sens où quelques méthodes standards suffisent à chaque catégorie de problèmes ( problèmes avec des polygones, problèmes avec des cercles ( il suffit par exemple de considérer sans perte de généralité que c'est le cercle unité ), problèmes qui font intervenir les notions de modulo et conjugué, problèmes polynomiaux, problèmes se résumant à la résolution d'équations trigonométriques etc.... ), c'est un livre orienté IMO .

Pour l'inversion : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=50&t=14958 ( c'est pas analytique et pas aussi fort, plutôt de la transfo + des propriétés remarquables ) .

par **Despo** » 16 Juin 2010, 16:10

Il me semble que j'avais deja entendu parlé de methodes "miracles" en geo.
Aprés l'arithmetique je pense qu'il ne peut pas y en avoir ,la combinatoire j'en ai jamais fait encore.Sinon y'a quelqu'un qui aurait des cours orientés oim en combinatoire?

par **poiuytreza** » 16 Juin 2010, 16:35

Déjà, les maths olympiques, ça s'apprend en cherchant des exos, pas en lisant des bouquins. Je ne connais pas le livre de Titu, mais ça m'étonnerait qu'il contienne tous les exos possibles et imaginables qui peuvent tomber aux IMO.
Ensuite, Mathlinks est une excellente base de donnée d'exercices, que j'utilise aussi beaucoup. Par contre, les gens dessus sont parfois bizarres et la proportion de solution fausse est assez effrayante, donc c'est pas parce que quelqu'un commence une solution avec des complexes que la solution est juste.
Enfin, l'inversion est une technique parmis d'autres, mais c'est pas de la force brute comme peut l'être l'analytique.
Et un dernier truc pour les complexes, si il y a 2 cercles, on prend 2 cercles unité ? :we:

par **Despo** » 16 Juin 2010, 20:12

C'est vrai mais il me semble que meme si la majorité des exos de geometrie sont resolvable avec les nombres complexes ce n'est pas facile pour autant(enfin je dit ca j'en sais rien mais je pense que c'est dur quand meme).Sinon pour faire les exos, faut des cours quand meme avant de pouvoir faire les exos ,mais pour ca les cours d'animath sont trés bien :cours+exos de differente difficulté.Mais il n y a pas de combinatoire c'est pour ca que j'aimerais avoir des cours de combinatoire orienté oim^^

par **Zweig** » 16 Juin 2010, 20:58

Eh non Olympus, les complexes ont des limites !

The bigest difficulties in the use of themethod of complex numbers can be encounteredwhen dealing with the intersection of the lines (as we can see from the fifth part of the theorem 2, although it dealt with the chords of the circle). Also, the difficulties may arrise when we have more than one circle in the problem. Hence you should avoid using the comples numbers in problems when there are lot of lines in general position without some special circle, or when there are more then two circles. Also,
the things can get very complicated if we have only two circles in general position, and only in the rare cases you are advised to use complex numbers in such situations. The problems when some of the conditions is the equlity with sums of distances between non-colinear points can be very difficult
and pretty-much unsolvable with this method. Of course, these are only the obvious situations when you cant count on help of complex numbers.
There are numerous innocent-looking problems where the calculation can give us increadible difficulties.

http://www.imomath.com/tekstkut/cnum_mr.pdf

Sinon dans le livre de Titu, c'est ni plus ni moins que de la géométrie complexe que l'on voit au Lycée ... Il y a juste quelques résultats supplémentaires comme l'intersection de deux droites, de deux cercles, les affixes de points remarquables etc ... Bref, la plupart du temps, tu ne t'en serviras jamais ...

par **Olympus** » 16 Juin 2010, 22:42

Ben si vous le dites, mea culpa !

N'empêche que j'ai vu pas mal d'exos de géométrie se faire torcher avec les complexes ( exemple, le dernier exo des IMO 2005 : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=267&t=44574 , page 2 et aussi voici un .pdf qui liste des exemples d'exos d'olympiade qui se font résoudre avec les complexes : http://web.mit.edu/yufeiz/www/wc08/peng_pset.pdf ), mais peut-être que ce n'étaient que des exos simples, ou alors comme l'a dit poiuytreza, les solutions sont peut-être fausses ou incomplètes .

par **Ben314** » 16 Juin 2010, 23:20

Les complexes, c'est l'UN des outils à maitriser pour faire de la géométrie, mais ce n'est en rien la panacé : c'est inutile sur les problèmes affines (style Thales), totalement inefficace sur les problèmes liés au projectif (Ménélaüs et son dual projectif Céva) et monstrueusement calculatoire sur tout ce qui concerne les coniques.
Le seul cas où c'est vraiment utile, c'est dans des problèmes que l'on peut traiter par compositions de similitudes (surtout directes)

P.S. : ce que tu appelle "géométrie invertive", visiblement, c'est ce que l'on appelle en français des inversions : ce sont des fonction particulières du groupe dit "circulaire" contenant les homographies de la droite projective complexe.
C'est effectivement UN des autres outil à maitriser pour simplifer beaucoup de problèmes d'intersections droites/cercles.

par **Despo** » 17 Juin 2010, 01:05

Ben314 a écrit:Les complexes, c'est l'UN des outils à maitriser pour faire de la géométrie, mais ce n'est en rien la panacé : c'est inutile sur les problèmes affines (style Thales), totalement inefficace sur les problèmes liés au projectif (Ménélaüs et son dual projectif Céva) et monstrueusement calculatoire sur tout ce qui concerne les coniques.
Le seul cas où c'est vraiment utile, c'est dans des problèmes que l'on peut traiter par compositions de similitudes (surtout directes)

P.S. : ce que tu appelle "géométrie invertive", visiblement, c'est ce que l'on appelle en français des inversions : ce sont des fonction particulières du groupe dit "circulaire" contenant les homographies de la droite projective complexe.
C'est effectivement UN des autres outil à maitriser pour simplifer beaucoup de problèmes d'intersections droites/cercles.

Mais il me semble vrai qu'avec ces 2 outils ,on peut resoudre la quasi totalité des exos de geo d'olympiades.Peut etre avec des solutions longues voire trés longues mais je pense qu'on peut toujours utilisé une solution avec les nombres complexes au dernier recours.Ca ferait quand meme 2 domaines des olympiades qui utiliserait des methodes qui marcherait a tous les coups .Peut etre existe t'ils aussi des methodes en arithmetique ou en combinatoire?Ce qui gacherait un peu les oim. :happy2:

par **benekire2** » 17 Juin 2010, 08:33

Salut !

Pour ton problème ben, je suis presque certain qu'il doit exister une solution archi-laide avec les complexes, si on prend le cercle circonscrit comme cercle unité. Je suis sur qu'un fou des complexes y parviendrait. Cela dit c'est moche ....

par **miikou** » 17 Juin 2010, 09:18

salut

j'ai parler de ce genre de technique car en realité ( et je ne doute pas que le verra bientot :id: ) se sont les plus utilisés. Bien sur les ineg données par les fonctions convexes ( dailleurs ca vient de la l'IAG si tu veux regarder .. ) sont bonnes a savoir !

jfais une tentative "olympique"

a+b+c=1

d'apres la forume de heron la surface du triangle vaut donc

l'inegalité isoperimetrique donne P² > 4pi S²

ici ca fait

(a+b+c)² > 2 pi (0.5-a)(0.5-b)(0.5-c)

ce qui donne

4(a+b+c)² > pi(1-2a)(1-2b)(1-2c)

et la ca merde :briques:

par **Olympus** » 17 Juin 2010, 10:16

miikou a écrit:salut

j'ai parler de ce genre de technique car en realité ( et je ne doute pas que le verra bientot :id: ) se sont les plus utilisés. Bien sur les ineg données par les fonctions convexes ( dailleurs ca vient de la l'IAG si tu veux regarder .. ) sont bonnes a savoir !

jfais une tentative "olympique"

a+b+c=1

d'apres la forume de heron la surface du triangle vaut donc

l'inegalité isoperimetrique donne P² > 4pi S²

ici ca fait

(a+b+c)² > 2 pi (0.5-a)(0.5-b)(0.5-c)

ce qui donne

4(a+b+c)² > pi(1-2a)(1-2b)(1-2c)

et la ca merde :briques:

Ce serait pas l'inégalité de Weitzenböck ( celle que je t'avais donné en MP ) que tu es en train d'essayer de prouver ?

PS : pour l'IAG, elle se prouve aussi par récurrence ( et tous les cas particuliers par réécriture sous forme de somme de carrés ^^ ) :we:

par **miikou** » 17 Juin 2010, 10:19

non je tentais ton ineg 1)

concernant le mp jte repond dans l'aprem ( mais oui bienvu je me sert de heron :D )

ps: je viens de relire ton MP, tu me parles de heron : ya meme plus de merite c'est assez immediat !

par **Olympus** » 17 Juin 2010, 10:28

Ah, sinon pour les inégalités avec les longueurs des côtés d'un triangle, ben la règle d'or est la substitution de Ravi .

En fait, si

sont les longueurs de côtés d'un triangle, alors selon l'inégalité triangulaire, il existerait des réels strictement positifs

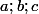
tels que :

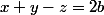
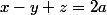
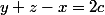
Tu résouds ce système d'inconnus

et t'auras :

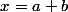
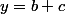
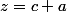
Et hop une fois fait la substitution, tu te seras débarassé de la contrainte "x;y;z sont les longueurs de côtés d'un triangle", et tu n'auras qu'à prouver une inégalité avec de simples réels positifs .

par **miikou** » 17 Juin 2010, 12:00

mdr on peut resoudre sans avoir la solution ?
ca allege bcp le "defi"

par **Olympus** » 17 Juin 2010, 13:23

miikou a écrit:mdr on peut resoudre sans avoir la solution ?
ca allege bcp le "defi"

Euh comment ça "sans avoir la solution" ?

Sinon, ouép, avec cette substitution + quelques égalités géométriques connues ( Formule de Héron etc... ), on peut torcher la plupart des inégalités géométriques vu que ça revient à montrer des inégalités ( souvent polynomiales ) avec des réels positifs . Bien sûr, cela ne marche pas sur certaines inégalités purement géométriques .

par **Despo** » 17 Juin 2010, 14:17

J'ai une question les inegalités geometrique rentre dans la case des inegalités ou dans celle de la geometrie? :we:

par **Olympus** » 17 Juin 2010, 14:33

Despo a écrit:J'ai une question les inegalités geometrique rentre dans la case des inegalités ou dans celle de la geometrie? :we:

D'après le nom, les deux :we:

Car on utilise quand même des résultats géométriques pour montrer qu'il suffit de démontrer une inégalité avec des réels positifs .

par **Despo** » 17 Juin 2010, 14:51

Ce qui les rends encore plus difficile^^
Merci de la reponse.

par **benekire2** » 17 Juin 2010, 20:35

Une question :

Bon alors c'est pas a propos des transformations de ravi (je connais) mais a propos des inégalités. l'IAG je connais. Mais je lis souvent chez toi olympus des "AM-GM pondéré" c'est quoi au juste ?

Merci ;)

Application de l'homogénéisation

Qui est en ligne