un groupe de n personne (n=<3) jouent au jeu suivant:
chacune d'entres elles lance une piece de monnaie non truqué.
un joueur gagne si tous les joueurs ont une resultat contraire au sien.
par exemple, le premier joueur gagne s'il obtient face et tous les autres pile
1-quelle est la probabilite qu'un joueur gagne
2-soit X la variable aleatoire qui compte le nombre de parties necessaires
pour avoir un gagnant.
a- determiner la loi de X
b-quelle est la probabilite que le premier gagnant apparait au 5eme jeu
c-le jeu sera fini neant si on arrive a la 10eme tours sans aucun gagnant
quel est la probabilite que le jeu soit fini neant
s'il vous plait c'est un cas tres urgent
Un exercice de probabilite treees difficile
7 messages
- Page 1 sur 1
Salut,
Vu ce que je comprend de la question 1), pour qu'un joueur gagne, il faut que le tirage soit du type (P,...,P,F,P,...P) [n possibilités] ou bien du type (F,F,...,F,P,F,...,F) [n possibilités].
Il y a donc 2n tirages qui permettent à un joueur de gagner et, comme chacun de ces tirages a une proba. de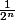 de sortir, cela donne une proba de
de sortir, cela donne une proba de  qu'un des joueurs gagne.
qu'un des joueurs gagne.
Pour la 2) il suffit de voir que, pour que X=k, il faut que les k-1 premières parties ne soient pas gagnantes et que la k-ième le soit donc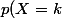=(1-p)^{k-1}\times p)
Pour la b, il suffit de prendre k=5 et, pour la c) de calculer^10)
Vu ce que je comprend de la question 1), pour qu'un joueur gagne, il faut que le tirage soit du type (P,...,P,F,P,...P) [n possibilités] ou bien du type (F,F,...,F,P,F,...,F) [n possibilités].
Il y a donc 2n tirages qui permettent à un joueur de gagner et, comme chacun de ces tirages a une proba. de
Pour la 2) il suffit de voir que, pour que X=k, il faut que les k-1 premières parties ne soient pas gagnantes et que la k-ième le soit donc
Pour la b, il suffit de prendre k=5 et, pour la c) de calculer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
1)
Est ce que c'est un joueur quelconque qui doit gagner ou un joueur precis ou encore un joueur precis et lqui gagne s'il obtient face et tous les autres pile...?
Dernier cas c'est ce que j'ai donné
deuxième cas c'est 2 fois ça (PFFFF...) ou (FPPPP...) c.a.d 2/2^n
premier cas, comme on a n joueur c'est n fois ça c.a.d 2n/2^n soit bien n/2^(n-1)
Est ce que c'est un joueur quelconque qui doit gagner ou un joueur precis ou encore un joueur precis et lqui gagne s'il obtient face et tous les autres pile...?
Dernier cas c'est ce que j'ai donné
deuxième cas c'est 2 fois ça (PFFFF...) ou (FPPPP...) c.a.d 2/2^n
premier cas, comme on a n joueur c'est n fois ça c.a.d 2n/2^n soit bien n/2^(n-1)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
