Exercice Fonction exponentielle, fonction cosinus

[Childou]

Bonjour,
je ne comprends la correction de mon exos.
On a f(x)=
Dans la question il est demandé de déterminer les abscisses des points d'intersection de Cf avec l'axe des abscisses.
Et voici le corrigé:
"Pour tout x, f(x)=0 équivaut à cosx=0 car la fonction exponentielle ne s'annule pas sur .
Les abscisses des points d'intersection de Cf avec l'axe des abscisses sont les réels ."
Et je ne comprends pas comment on arrive à ce résultat, quelqu'un pourrait-il m'expliquer?
Merci d'avance.

[Arnaud-29-31]

Bonsoir,

Qu'est-ce qui te bloque ?

Le fait que chercher les abscisses des points d'intersections de Cf avec l'axe des abscisses revient à résoudre f(x) = 0 ? Le fait que f(x) = 0 est équivalent à cos(x) = 0 ? Ou bien les solutions de cos(x) = 0 ?

[Hiphigenie]

Bonjour,


.

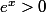
Tu sais que pour tous les réels x. Donc pour tous les réels x.

On peut alors diviser les deux membres de l'équation par .

Cette équation devient : .

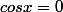
De plus

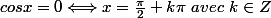
C'est cette dernière équivalence qui te pose un problème ?

[Childou]

Oui, je ne comprend pas comment on trouve

[Hiphigenie]

Regarde sur le cercle trigonométrique les valeurs de x telles que cos x = 0.

[Hiphigenie]

Que valent : ?

[Dinozzo13]

Salut !
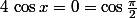
équivaut à
ou .
De là, tu remarques que l'on peut synthétiser :
et sous la forme :

[Childou]

D'accord je viens de comprendre, on prend tout les valeurs pour lesquelles cosx=0 en fait.
Mais je ne vois pas le rapport entre les abscisses des points d'intersection de Cf avec l'axe des abscisses. Je n'arrive pas à visualiser ce qu'on me demande.

[Hiphigenie]

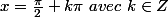
Tu es d'accord que les valeurs de x dont nous parlons (c'est-à-dire ) sont bien les solutions de l'équation .

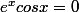
Ce sont donc les solutions de l'équation .

Autrement dit, ce sont les valeurs de x dont les images par la fonction sont nulles ou encore ce sont les valeurs de x pour lesquelles le graphique Cf de la fonction coupe l'axe des abscisses.

Comme le dit l'énoncé, ce sont les abscisses des points d'intersections entre le graphique Cf de la fonction et l'axe des abscisses.