Equation différentielle ordinaire

[mengde]

Bonjour à tous

voila je suis en train de chercher a résoudre cet exercice:

Résoudre l'edo suivante:

[CENTER]x'(t) - x(t) = x^1/2

x(0) = 0[/CENTER]

1: montrer que y(t) = 1/x(t) satisfait une edo linéaire

2: la résoudre en y(t)

3: obtenir la solution de l'équation en x (t)


Honnétenment je suis en panne d'inspiration, j'avais pensais a une edo de bernoulli.... mais sans conviction..... :mur:

si vous pouvez m'aider, je vous en serez trés reconnaissant!!!!

[buzard]

C'est bien du bernoulli, mais je ne suis pas sûre pour ton changement de variable, c'est plutot
c'est sûrement pour ça que tu n'avance pas.

[EDIT] désolé le chgmt c'est comme quoi se relire c'est parfois utile

[mengde]

j'aimerais bien sauf que c'est dans l'enoncé le fameux y = 1/x(t) :cry:

[buzard]

c qu'il y a une coquille dans l'énoncé, il a du copier coller les question depuis une autre equa diff où le membre de droite devait etre x^2, ça m'étonnerai pas que ce soit la question précédente :p

[mengde]

c qu'il y a une coquille dans l'énoncé, il a du copier coller les question depuis une autre equa diff où le membre de droite devait etre x^2, ça m'étonnerai pas que ce soit la question précédente :p

mdr si c'est vrai :we:

[valentin.b]

Bonjour,

C'est pas dans l'énoncé, mais ça se justifie ...

On écrit de façon générale qu'on a le changement de variable :


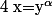
Bien sur alpha différent de 0 ...
Donc :


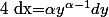
Ainis l'équation différentielle devient :


Ca devient :


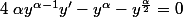
En mettant en facteur puisque le terme n'est à priori pas toujour nul, on a :


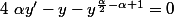
Ou :


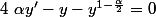
On sait résoudre facilement quand

Ce qui rejoint ce qui a été posé