Bonjour,
J'ai un petit probleme pour résoudre cet exo de centrale tombé à l'oral l'année derniere... Je déteste ce genre d'exercices ! Tellement théorique que je ne comprends pas ce qui est demandé. Pourriez-vous me donner des indications ?
E un espace vectoriel euclidien. (e1,e2,...,en) une base de E
a) Montrer que Phi : E ->R^n , x-> ((e1/x),...,(en/x)) est un isomorphisme.
( (./.) produit scalaire)
Bon ça je pense avoir trouvé.
b) soit (f1..fn) une base de E verifiant
pour tout x appartenant à E, x = sum( (ei/x)*fi , i=1..n) (P)
calculer (ei/fj)
Et la... je ne comprends pas vraiment ce qu'on demande. Quel est l'interet de calculer ce produit scalaire ? en remplacant x par ei je trouve
(ei/fj) = sum( (ei/ek)*(fk/fj) , k=1..n)
Est-ce ce qui est attendu ?
Et enfin la derniere question :
c) montrer qu'il existe une unique base (f1...fn) verifiant (P)
Je suppose qu'il faut utiliser l'isomorphisme du 1, mais franchement, je suis perdue...
Merci d'avance
Exercice centrale : aie
10 messages
- Page 1 sur 1
Je ne vois pas l'utilité de la question 2.
En effet, elles ne sont pas orthonormé, c'est même essentiel.
Si tu prends deux bases (fi) et (f'i) qui vérifient ça. Alors les coordonnées de tous les vecteurs sont les même dans ces deux bases. LA coordonnée de x suivant fk est (ek|x).
Donc on vérifie que l'identité est un iso de l'esp muni de la première base vers l'esp muni de la seconde en passant par la question 1.
C'est un exo de formalisme. Un peu space.
En effet, elles ne sont pas orthonormé, c'est même essentiel.
Si tu prends deux bases (fi) et (f'i) qui vérifient ça. Alors les coordonnées de tous les vecteurs sont les même dans ces deux bases. LA coordonnée de x suivant fk est (ek|x).
Donc on vérifie que l'identité est un iso de l'esp muni de la première base vers l'esp muni de la seconde en passant par la question 1.
C'est un exo de formalisme. Un peu space.
Salut,
Si tu veut mon avis, vu l'énoncé, seul la base de départ (e1,e2,...,en) est "connue" donc, lorsque l'on demande à la question b) de "calculer ", il faut que le résultat ne dépende que des ei et à la rigueur de la fonction Phi introduite précédement, mais surement pas des f? !!!
(Par exemple, l'étudiant qui écrit vaut... , bien qu'il ait répondu à la question et que sa réponse soit juste, ben je pense qu'il a 0 à la question !!!)
Comme par hypothèse, pour tout x de E on a x = sum( (ei/x)*fi , i=1..n) alors, en prenant x=fj, tu en déduit que fj = sum( (ei/fj)*fi , i=1..n)
Sauf que (f1,f2,...,fn) est une base donc il existe une unique écriture de fj comme combinaison linéaire de f1,f2,...fn qui est évidement fj=...
Donc, comme on a aussi fj = sum( (ei/fj)*fi , i=1..n), on en déduit que...
Si tu veut mon avis, vu l'énoncé, seul la base de départ (e1,e2,...,en) est "connue" donc, lorsque l'on demande à la question b) de "calculer ", il faut que le résultat ne dépende que des ei et à la rigueur de la fonction Phi introduite précédement, mais surement pas des f? !!!
(Par exemple, l'étudiant qui écrit vaut... , bien qu'il ait répondu à la question et que sa réponse soit juste, ben je pense qu'il a 0 à la question !!!)
Comme par hypothèse, pour tout x de E on a x = sum( (ei/x)*fi , i=1..n) alors, en prenant x=fj, tu en déduit que fj = sum( (ei/fj)*fi , i=1..n)
Sauf que (f1,f2,...,fn) est une base donc il existe une unique écriture de fj comme combinaison linéaire de f1,f2,...fn qui est évidement fj=...
Donc, comme on a aussi fj = sum( (ei/fj)*fi , i=1..n), on en déduit que...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour Ben314
Merci pour ton aide. Grace à toi je comprends un peu mieux l'esprit de l'énoncé...
Je déduis de ce que tu m'as expliqué que pour tout i différent de j (ei/fj) = 0 et (ej/fj) =1.
Pour la question c), je ne vois pas le rapport avec la b).... Si tu pouvais m'éclairer ce serait très sympa.
Merci pour ton aide. Grace à toi je comprends un peu mieux l'esprit de l'énoncé...
Je déduis de ce que tu m'as expliqué que pour tout i différent de j (ei/fj) = 0 et (ej/fj) =1.
Pour la question c), je ne vois pas le rapport avec la b).... Si tu pouvais m'éclairer ce serait très sympa.
Le rapport, c'est que maintenant que tu connait les pour tout i, cela siginfie que tu connait Phi(fj) et comme a la question a) tu as montré que Phi est bijective, ça ne laisse pas beaucoup de possibilités pour fj.
Evidement, il faut montrer que, si on prend pour les différents fj les images réciproques par Phi des différents (0,...,0,1,0,...,0) c'est bien une base et qu'elle vérifie la propriétée (P).
Indication : comme Phi est bijective, pour montrer que deux éléments de E sont égaux, il suffit de montrer qu'ils ont la même image par Phi...
Evidement, il faut montrer que, si on prend pour les différents fj les images réciproques par Phi des différents (0,...,0,1,0,...,0) c'est bien une base et qu'elle vérifie la propriétée (P).
Indication : comme Phi est bijective, pour montrer que deux éléments de E sont égaux, il suffit de montrer qu'ils ont la même image par Phi...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour
un vecteur quelconque a des coordonnées
quelconque a des coordonnées 
si on définit l'application qui à
associe sa ième coordonnée
on s'aperçoit
i) que cette application est à valeurs dans R
ii) elle est linéaire
on parle d'une forme linéaire
il se trouve que cette application est aussi
 si la base est o.n
si la base est o.n
ces applications linéaires , notée ou
ou 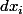
selon les auteurs forment une base de l'espace vectoriel des
formes linéaires
exemple: un hyperplan de d'équation
d'équation
3x+2y+5z=0 est le noyau d'une telle forme linéaire
si=3x+2y+5z) où
où )
alors
 est combinaison linéaire des ces formes "coordonnées" (c'est leur nom)
est combinaison linéaire des ces formes "coordonnées" (c'est leur nom)
un vecteur
si on définit l'application qui à
associe sa ième coordonnée
on s'aperçoit
i) que cette application est à valeurs dans R
ii) elle est linéaire
on parle d'une forme linéaire
il se trouve que cette application est aussi
ces applications linéaires , notée
selon les auteurs forment une base de l'espace vectoriel des
formes linéaires
exemple: un hyperplan de
3x+2y+5z=0 est le noyau d'une telle forme linéaire
si
alors
après, tu as ce que l'on appelle un "crochet de dualité"
l'idée c'est de mettre en valeur , dans l'expression f(x),
où x est un vecteur et f une forme linéaire , la double linéarité,
l'une par rapport au vecteur x , l'autre par rapport à la forme
on écrit alors
f(x)= linéaire relativement à chaque opérande
l'idée c'est de mettre en valeur , dans l'expression f(x),
où x est un vecteur et f une forme linéaire , la double linéarité,
l'une par rapport au vecteur x , l'autre par rapport à la forme
on écrit alors
f(x)= linéaire relativement à chaque opérande
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
