Etude d'une suite puissance

[AceVentura]

Bonjour,

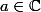
je dois étudier la monotonie et le comportement de la suite pour . Je vois déjà que si a=0 ou a=1, la suite est constante donc admet une limite finie égale à 0 ou 1.
Je n'arrive pas à synthétiser les différents autres cas.

Pouvez-vous me guider ?
Merci !

[Nightmare]

Salut,

hum, quel sens donner au mot "monotonie" pour une suite de complexes ?

[Ben314]

Salut,
Je te conseillerais de commencer par étudier la suite des modules de a^n qui, elle, a le bon gout d'être une suite réelle donc pour laquelle la notion de monotonie a un sens...

Rappel :Il n'y a pas de relation d'ordre naturelle dans C...

[AceVentura]

Il me semble naturelle de dire qu'une suite complexe est monotone si la suite réelle l'est, non ?

[Ben314]

Il me semble naturelle de dire qu'une suite complexe est monotone si la suite réelle l'est, non ?

A mon avis, il vaut nettement mieux dire directement que la suite est monotone : c'est pas les deux barres en plus qui ralongent bien l'écriture et au moins, il n'y a aucune ambigüité sur ce que ça veut dire...

[AceVentura]

Ok. Comment étudier la limite éventuelle ?

[alavacommejetepousse]

bonsoir
voila tout ce qu 'il faut dire :
1
si le module est strictement supérieur à 1 quid ?

2 idem si strict inf ?

3 si le module vaut 1 posez u(n) = a^n de u(n+1) = au(n) quelle CN doit vérifier a pour que la limite existe ?

[alavacommejetepousse]

Rappel :Il n'y a pas de relation d'ordre naturelle dans C...

hello ben
chipotons

il y en a une l'ordre lexicographique mais il n y en a aucune compatible avec la structure de corps

[Ben314]

...il y en a une l'ordre lexicographique mais il n y en a aucune compatible avec la structure de corps

O.K. (et c'est d'ailleurs pour ça que j'ai mis le mot "naturelle". L'ordre lexicographique n'est, à mon sens pas "naturel", ne cerais ce que parce qu'il demande de priviligier une des deux variables x ou y (dans z=x+iy) pour être défini et que cela ne peut être que totalement artificiel.

P.S. bien entendu, tout cela est un "jeux sur les mots" vu que je ne pense pas qu'il y ait de définitions carrée-carrée des mots "naturel" et "artificiel"...

[alavacommejetepousse]

O.K. (et c'est d'ailleurs pour ça que j'ai mis le mot "naturelle". L'ordre lexicographique n'est, à mon sens pas "naturel", ne cerais ce que parce qu'il demande de priviligier une des deux variables x ou y (dans z=x+iy) pour être défini et que cela ne peut être que totalement artificiel.

P.S. bien entendu, tout cela est un "jeux sur les mots" vu que je ne pense pas qu'il y ait de définitions carrée-carrée des mots "naturel" et "artificiel"...

allez jouons

si un complexe est un couple de réels il y a bien la première variable et la deuxième naturellement dans l'écriture européenne de la gauche vers la droite ? :id:

[chbichib khaled]

Le Corps Des Nombres Complexes Ne Pas Muni D'une Relation D'ordre ...QUI NOUS PERMET DE DÉFINIR LA MONOTONIE D'UNE SUITE ...ET SI çA EXISTE A MON AVIS IL FAUT REVENIR AU CORPS DE RÉELLE PAR L APPLICATION NORME

[alavacommejetepousse]

faut lire jusqu'au bout les posts


je le munis de la relation
z =< z' si a < a ' ou a= a ' et b =< b' pour z = a+ib et z ' = a'+ib'

elle te convient pas ?

[Finrod]

Ou la relation analogue avec les coordonnées polaires. Tu connais des domaines ou des relations sont utiles alava ?

[Finrod]

Ou la relation analogue avec les coordonnées polaires. Tu connais des domaines ou ces relations sont utiles alava ?

[AceVentura]

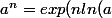Je n'arrive pas à étudier la suite ! ? Mais c'est quoi pour complexe ? (Même si je n'ai pas trop envie de partir la dessus, j'ai déjà un problème de définition)

Après, je n'ai pas de méthode pour étudier cette limite.

[AceVentura]

En fait non, il faut étudier la limite pour ! Je me suis trompé ! Cela semble être l'infini lorsque . Je n'arrive pas à le montrer clairement.

[Finrod]

Avant d'apprendre un jour le log complexe, tu as le temps.

Ta suite est de la forme avec

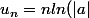calcule d'abord la limite de puis fais par composition.

[AceVentura]

En effet ! .
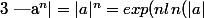Donc si , alors et donc et s'ensuit que .

De même, si (et et donc finalement !) alors et donc et s'ensuit que .

Maintenant si (ie ) alors elle est de limite nulle car la suite est constante égale à 0.

Enfin, si |a|=1, alors la suite est constante égale à 1, elle a donc pour limite 1.

[AceVentura]

Enfin, si |a|=1, alors la suite est constante égale à 1, elle a donc pour limite 1.

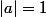
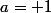
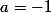
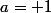
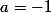
Je m'aperçois que ma dernière phrase est fausse ! Si , alors ou . Si , la suite est constante est converge vers 1 et si alors la suite est divergente !

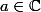
Finalement, pour , la suite (a^n)_n est :
divergente vers si
convergente vers 0 si
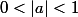
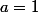
constante (donc convergente) si ou
divergente si .

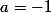
Que pensez-vous de la classification ?

[Ben314]

Ben, pour |a|<1 et pour |a|>1, ça semble O.K.
Par contre, pour |a|=1, ça me semble un peu réducteur de ne considérer que les deux cas a=1 et a=-1.
Que fait tu du cas où a=i ? et du cas où a=1/2+i.racine(3)/2 ? ...