Théorie des graphes

[Scipion]

Bonjour à tous,
Je voulais vous demander comment peut-on prouver qu'un graphe est planaire ? Est-ce que le théorème des 4 couleurs prouve qu'un graphe est planaire (donc que si nous pouvons colorer le graphe avec seulement 4 couleurs, celui-ci est planaire ?)

[Ben314]

Salut,
Non, le fait de pouvoir colorier un graphe en un certain nombre de couleurs ne risque pas d'impliquer qu'il est planaire :
Si tu part d'un graphe absolument quelconque et que tu intercalle un sommet au milieu de chaque arrète, le nouveau graphe obtenu est biparti donc peut se colorier avec seulement 2 couleurs (noir pour les sommets du graphe de départ et blanc pour ceux rajoutés au milieu des arrètes) or il est évident que ce nouveau graphe n'est planaire que si le graphe de départ l'était.

La caractérisation "classique" des graphes planaires est :
Un graphe est planaire ssi il ne contient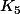 ni ni 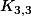parmi ces mineurs.

Et, une caractérisation des graphes coloriables avec 4 couleurs est :
Un graphe est coloriable avec 4 couleurs ssi il ne contient pas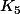 parmi ces mineurs.

[Ericovitchi]

la plus connue c'est la Caractérisation de Kuratowski et de Wagner (Un graphe fini est planaire si et seulement s'il ne compte pas K5 ou K3,3 parmi ses mineurs). Voir wikipedia

Par contre le lien avec le théorème des 4 couleurs, ça me dépasse. Il semble que des résultats de théorèmes sur les graphes planaires servent à démonter des choses utiles pour traiter des problèmes de coloration de cartes, mais je n'en sais pas plus.

Edit : Ha grillé par le grand Ben qui sait déjà ce que sont K5 et K3,3

[Ben314]

En fait, pour les k-coloriage, il y a la Conjecture d'Hadwiger :

Un graphe est k-coloriable ssi il ne contient pas parmi ces mineurs.

La conjecture est démontrée pour k=2,3,4,5 mais reste non démontrée pour k>5 (en fait, pour k=4 et k=5, la preuve se ramène au théorème des 4 couleurs)

[Scipion]

Yep j'avais déjà vu qu'il n'était pas planaire s'il était un homéomorphisme de K5 ou K3,3. OK je vais aller lire tout cela. Cependant, j'ai trouvé clairement inscris que si un graphe à plus de 4 couleurs il n'est pas planaire. Mais apparemment, selon vous l'inverse n'est pas valable (donc si j'ai 4 couleurs ou moins, ce n'est pas obligatoirement planaire).

[Ben314]

Dire que "si un graphe est planaire alors il est 4-coloriable", ça, c'est trés exactement le théorème des 4 couleurs.
La réciproque est trivialement fausse (cf mon premier post)