Suite géométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 05 Juin 2010, 16:28
par AceVentura » 05 Juin 2010, 16:28
Bonjour. Je voudrais étudier la convergence de la suite

sans utiliser l'écriture

sous la forme exponentielle, ni utiliser le critère de d'Alembert. Je dois me
ramener à une suite géométrique :
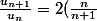^2)
. C'est presque la forme voulue
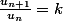
, mais ici j'ai
^2)
et
^2)
qui tend vers

. Comment faire ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Juin 2010, 16:39
par Nightmare » 05 Juin 2010, 16:39
Salut,
je pense que le plus simple est de montrer que

à partir d'un certain rang.
Une récurrence fait l'affaire :
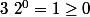
et
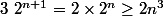
. Or
^{3}\sim_{n\infty} n^{3}\longrightarrow_{n\infty} +\infty)
donc à partir d'un certain rang
^{3})
et l'hérédité est assurée.
:happy3:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 05 Juin 2010, 16:46
par Finrod » 05 Juin 2010, 16:46
Essai de prendre
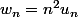
suite géo de para 2
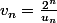
vérifiant
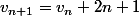
Alors vérifie

Il suffit d'étudier la limite du quotient des deux suites or
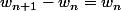
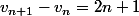
Il faut montrer que
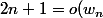)
alors en regardant
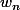
comme la série de terme général
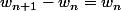
et

comme la série de terme général
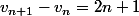
on en déduit par croissance comparé que
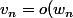)
soit que
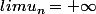
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Juin 2010, 16:49
par Nightmare » 05 Juin 2010, 16:49
Sinon, avec ce que tu as déjà fait :
[n/(n+1)]² tend vers 1 donc est supérieur à 3/4 à partir d'un certain rang, d'ou

à partir d'un certain rang N, puis
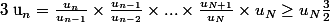^{n-N-1}\;\;\longrightarrow_{n\infty}\; +\infty)
(car u(N) > 0)
:happy3:
-
vingtdieux
- Membre Relatif
- Messages: 196
- Enregistré le: 27 Mai 2010, 22:22
-
 par vingtdieux » 05 Juin 2010, 16:51
par vingtdieux » 05 Juin 2010, 16:51
Comprends pas on peut voir que cette suite tend vers l'infini quand n tend vers l'infini. J'utilise deux fois la regle de l'hospital pour la forme indeterminée. (et aussi a^x=e^xlna)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 05 Juin 2010, 16:59
par AceVentura » 05 Juin 2010, 16:59
Ok, je crois que ce qui est attendu ici est ce qu'a dit Nightmare ! Pour vingtdieux, on demande de passer par les suites géométriques, j'y peux rien ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 129 invités
 sans utiliser l'écriture
sans utiliser l'écriture  sous la forme exponentielle, ni utiliser le critère de d'Alembert. Je dois me ramener à une suite géométrique :
sous la forme exponentielle, ni utiliser le critère de d'Alembert. Je dois me ramener à une suite géométrique :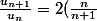^2) . C'est presque la forme voulue
. C'est presque la forme voulue 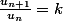 , mais ici j'ai
, mais ici j'ai ^2) et
et ^2) qui tend vers
qui tend vers  . Comment faire ?
. Comment faire ?