Comparaison de suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 04 Juin 2010, 15:45
par AceVentura » 04 Juin 2010, 15:45
Bonjour,
toujours des petites questions sur les suites.
(i) Je veux prouver que si deux suites réelles
)
et
)
convergent respectivement vers les réels

et
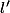
, et s'il existe un
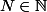
tel que

, alors

.
Preuve :
Donc dès que
)
, on a

et après je ne vois pas comment avoir l'inégalité avec

!
(ii) Je souhaite prouver le théorème d'encadrement : si à partir de
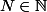
,

et si

, alors

.
Preuve :Même chose, dès que
)
on a

et donc en particulier |

. Est-ce correct ?
Merci encore !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Juin 2010, 15:53
par Ben314 » 04 Juin 2010, 15:53
Pour le i), (en prenant

) tu as montré que :

c'est à dire

ce qui prouve que

(la contraposée est triviale)
Pour le ii), c'est O.K.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 04 Juin 2010, 15:59
par AceVentura » 04 Juin 2010, 15:59
Ben314 a écrit:
c'est à dire

ce qui prouve que

(la contraposée est triviale)
Pourquoi :hein:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 04 Juin 2010, 19:28
par Finrod » 04 Juin 2010, 19:28
Parce que c'est vrai pour tout

strictement positif.
Par contraposée si
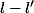
est strictement positif, il existe un

positif, par ex
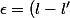/2)
plus petit que
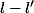
.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 04 Juin 2010, 19:42
par AceVentura » 04 Juin 2010, 19:42
Merci beaucoup

(désolé Ben, j'ai mal interprété le "
la contraposée est triviale")
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités