Algorithme
20 messages
- Page 1 sur 1
Algorithme
Bonjour à tous,
J'espère que vous allez bien ! Les vacances approchent ... pour ma part c'est dans 2 semaines :)
J'ai tout de même, pour finir en beauté, un dernier DM où un exercice m'embête ... Toujours les algorithmes !
Voici l'énoncé :
Ecrire sous forme codée l'algorithme qui permet de tester l'alignement de trois points A, B et C lorsqu'on connaît les coordonnées des points A, B et C dans un repère.
Je dois utiliser les formules pour calculer des coordonnées d'un vecteur, je pense :
vAB = xA - xB
yA - yB
Non ?
Je ne vois pas en tout cas comment écrire un algorithme pour répondre à l'énoncé ...
Je compte sur vous pour m'expliquer :D
Bonne journée
J'espère que vous allez bien ! Les vacances approchent ... pour ma part c'est dans 2 semaines :)
J'ai tout de même, pour finir en beauté, un dernier DM où un exercice m'embête ... Toujours les algorithmes !
Voici l'énoncé :
Ecrire sous forme codée l'algorithme qui permet de tester l'alignement de trois points A, B et C lorsqu'on connaît les coordonnées des points A, B et C dans un repère.
Je dois utiliser les formules pour calculer des coordonnées d'un vecteur, je pense :
vAB = xA - xB
yA - yB
Non ?
Je ne vois pas en tout cas comment écrire un algorithme pour répondre à l'énoncé ...
Je compte sur vous pour m'expliquer :D
Bonne journée
deux vecteurs colineaires ne traduisent pas forcément des points alignés.
Ex : un parallelogramme abcd, (ab) parallele à (cd) pourtant a b et c ne sont pas alignés.
i faut un point commun.
Pour lalgo ben c'est tu veux en fait montrer
MP = k MQ, avec MP et MQ des veecteurs, k un scalaire.
Tu peux reecrire ca
k = (xP-xM)/(xQ-xM)
si tu trouves le meme k pour (yP-yM)/(yQ-yM), alors c'est que c'est les vecteurs sont colinaires et tes points alignés.
Faut faire gaffe a la division par zero... :)
Ex : un parallelogramme abcd, (ab) parallele à (cd) pourtant a b et c ne sont pas alignés.
i faut un point commun.
Pour lalgo ben c'est tu veux en fait montrer
MP = k MQ, avec MP et MQ des veecteurs, k un scalaire.
Tu peux reecrire ca
k = (xP-xM)/(xQ-xM)
si tu trouves le meme k pour (yP-yM)/(yQ-yM), alors c'est que c'est les vecteurs sont colinaires et tes points alignés.
Faut faire gaffe a la division par zero... :)
la vie est une fête 
En effet 2 vecteurs colinéaires ne traduisent pas forcément des points alignés, pourtant dans l'exemple du cours ma prof a écrit une formule où on obtient 0 donc les vecteurs sont colinéaires, donc les points sont alignés mais ce doit être que dans certains cas !
Désolée de ne pas avoir répondu avant, j'avais des concerts pour la fête des mères. Du coup je suis assez en retard & je ne comprends toujours pas ... J'espère trouver l'algorithme d'ici mardi :S
Je n'ai pas très bien compris l'explication ; rien que la première phrase je ne vois pas pourquoi "k" intervient. Qu'est-ce qu'un "scalaire" ?
Suite à votre explication, je ne retrouve pas l'application du cours ... J'espère que vous verrez ce message :S
Désolée de ne pas avoir répondu avant, j'avais des concerts pour la fête des mères. Du coup je suis assez en retard & je ne comprends toujours pas ... J'espère trouver l'algorithme d'ici mardi :S
Je n'ai pas très bien compris l'explication ; rien que la première phrase je ne vois pas pourquoi "k" intervient. Qu'est-ce qu'un "scalaire" ?
Suite à votre explication, je ne retrouve pas l'application du cours ... J'espère que vous verrez ce message :S
fatal_error a écrit:deux vecteurs colineaires ne traduisent pas forcément des points alignés.
Ex : un parallelogramme abcd, (ab) parallele à (cd) pourtant a b et c ne sont pas alignés.
i faut un point commun.
Pour lalgo ben c'est tu veux en fait montrer
MP = k MQ, avec MP et MQ des veecteurs, k un scalaire.
Tu peux reecrire ca
k = (xP-xM)/(xQ-xM)
si tu trouves le meme k pour (yP-yM)/(yQ-yM), alors c'est que c'est les vecteurs sont colinaires et tes points alignés.
Faut faire gaffe a la division par zero...
Par rapport à mon énoncé ; où sont les points A, B et C ?
Bonjour,
fatal_error a voulu te guider sans te donner la solution,
donc il a parlé de manière générale.
Il suffit de remplacer ses points P, Q et R par tes points A, B et C.
Et pour utiliser la colinéarité pour prouver l'alignement, il faut un point commun comme te l'a dit fatal_error.
* et
et 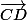 sont colinéaires implique (AB)//(CD)
sont colinéaires implique (AB)//(CD)
* et
et  sont colinéaires implique (AB)//(AC) implique (AB) et (AC) sont confondues grâce au point commun A implique A, B et C sont alignés
sont colinéaires implique (AB)//(AC) implique (AB) et (AC) sont confondues grâce au point commun A implique A, B et C sont alignés
fatal_error a voulu te guider sans te donner la solution,
donc il a parlé de manière générale.
Il suffit de remplacer ses points P, Q et R par tes points A, B et C.
Et pour utiliser la colinéarité pour prouver l'alignement, il faut un point commun comme te l'a dit fatal_error.
*
*
J'ai remplacé les lettres par A B et C
Mais le problème reste toujours le même ; comment le mettre sous forme d'algorithme ...
Entrée : Saisir quoi ?
Traitement : k = (xB - xA) / ( xC - xA)
Si k = ( yB - yA) / ( yC - yA )
Alors AB et AC sont colinéaires
Sortie : ?
Je sais très bien que c'est faux mais je ne sais pas comment mettre sous forme d'algorithme :S
Mais le problème reste toujours le même ; comment le mettre sous forme d'algorithme ...
Entrée : Saisir quoi ?
Traitement : k = (xB - xA) / ( xC - xA)
Si k = ( yB - yA) / ( yC - yA )
Alors AB et AC sont colinéaires
Sortie : ?
Je sais très bien que c'est faux mais je ne sais pas comment mettre sous forme d'algorithme :S
Pauuline a écrit:J'ai remplacé les lettres par A B et C
Mais le problème reste toujours le même ; comment le mettre sous forme d'algorithme ...
Entrée : Saisir quoi ?
Bin tu dois saisir les nombres que tu utilises dans le traitement !
Comment veux tu que l'algorithme te dise si les points sont alignés si ton algorithme ne connait pas les coordonnées des points ?
Pauuline a écrit:Traitement : k = (xB - xA) / ( xC - xA)
Si k = ( yB - yA) / ( yC - yA )
Alors AB et AC sont colinéaires
Sortie : ?
Bin la sortie c'est la réponse à la question, c'est-à-dire "oui, les points sont alignés" ou bien "non, les points ne sont pas alignés"
Pauuline a écrit:Je sais très bien que c'est faux mais je ne sais pas comment mettre sous forme d'algorithme :S
Non, ce n'est pas faux, c'est juste incomplet.
Fais attention à ce que t'a dit fatal_error : attention à la division par 0 ;
si A et C ont la même abscisse ou bien la même ordonnée, ton algorithme va planter car dans ton traitement il y aura une division par zéro.
Soit tu testes l'égalité pour traiter ce cas à part, soit tu traduis la proportionnalité des coordonnées des vecteurs
gigamesh a écrit:Bin tu dois saisir les nombres que tu utilises dans le traitement !
Comment veux tu que l'algorithme te dise si les points sont alignés si ton algorithme ne connait pas les coordonnées des points ?
Bin la sortie c'est la réponse à la question, c'est-à-dire "oui, les points sont alignés" ou bien "non, les points ne sont pas alignés"
Non, ce n'est pas faux, c'est juste incomplet.
Fais attention à ce que t'a dit fatal_error : attention à la division par 0 ;
si A et C ont la même abscisse ou bien la même ordonnée, ton algorithme va planter car dans ton traitement il y aura une division par zéro.
Soit tu testes l'égalité pour traiter ce cas à part, soit tu traduis la proportionnalité des coordonnées des vecteurset
par l'égalité des produits en croix, ce qui évite les divisions.
Moi j'avais appris avec les produits en croix donc ce serait mieux que je les utilise car je ne comprenais pas la division ... Donc si je récapitule :
Entrée : Saisir A
Saisir B
Saisir C
Faut-il que je précise xA ; xB ; yA ; yB ... ?
Traitement :
k = xb * ya - xa * yb
Si k = xc * ya - xa / yc
Alors AB et AC sont colinéaires
Le seul problème ici c'est que c'est 2x le nombre k
Je voudrais plutot dire si xb * ya - xa * yb = xc * ya - xa / yc
Alors les vecteurs sont colinéaires.
En lisant ce que j'ai écrit, c'est ce que vous comprenez
Sortie : Oui les points sont alignés
Non les points ne sont pas alignés
A-t-on le droit de mettre des phrases en sortie ?
Pauuline a écrit:Moi j'avais appris avec les produits en croix donc ce serait mieux que je les utilise car je ne comprenais pas la division ... Donc si je récapitule :
Entrée : Saisir A
Saisir B
Saisir C
Faut-il que je précise xA ; xB ; yA ; yB ... ?
Oui, il faut demander l'abscisse et l'ordonnée de chaque point.
Pauuline a écrit:Traitement :
k = xb * ya - xa * yb
Si k = xc * ya - xa / yc
Alors AB et AC sont colinéaires
Hum...
Pour les produits en croix, on utilise les coordonnées des vecteurs , pas les coordonnées des points.
Pauuline a écrit:
Le seul problème ici c'est que c'est 2x le nombre k
Je voudrais plutot dire si xb * ya - xa * yb = xc * ya - xa / yc
Je ne comprends pas cette formule.
Pauuline a écrit:Alors les vecteurs sont colinéaires.
En lisant ce que j'ai écrit, c'est ce que vous comprenez
Sortie : Oui les points sont alignés
Non les points ne sont pas alignés
A-t-on le droit de mettre des phrases en sortie ?
Oui, on peut. vu que la question résolue par l'algorithme a une réponse OUI/NON, on va pas répondre 42 ou 7,8, de toutes façons...
Exact,
on n'a pas les coordonnées des vecteurs.
Mais on sait les calculer :
La formule) signifie que pour calculer les coordonnées d'un vecteur, on prend les coordonnées du point d'arrivée et on soustrait les coordonnées du point de départ.
signifie que pour calculer les coordonnées d'un vecteur, on prend les coordonnées du point d'arrivée et on soustrait les coordonnées du point de départ.
Le mieux est d'essayer l'algorithme sur un exemple, pour voir.
Entrée A(5;7) B(9;4) C(14;0)
Traitement
* On calcule les coordonnées de
 et
et donc
donc )
* On calcule les coordonnées de
à toi de jouer...
* On teste l'égalité des produits en croix \times ... =...)
Sortie
si différence =0
alors
ecrire "points alignés"
sinon
ecrire "points pas alignés"
on n'a pas les coordonnées des vecteurs.
Mais on sait les calculer :
La formule
Le mieux est d'essayer l'algorithme sur un exemple, pour voir.
Entrée A(5;7) B(9;4) C(14;0)
Traitement
* On calcule les coordonnées de
* On calcule les coordonnées de
à toi de jouer...
* On teste l'égalité des produits en croix
Sortie
si différence =0
alors
ecrire "points alignés"
sinon
ecrire "points pas alignés"
En clair le traitement c'est :
vAB = (xb - xa ; yb - ya)
vAC = (xc - xa ; yc - ya)
Si xb-xa * yc-ya - xc-xa * yb-ya = 0
alors
ecrire "points alignés"
sinon
ecrire "points pas alignés"
Sortie : Fin de Si
J'ai vraiment du mal à comprendre ; même si je connais la formule pour la mettre sous forme d'un algorithme c'est plus dur ! Je suis désolée si je donne l'impression de ne rien comprendre ...
vAB = (xb - xa ; yb - ya)
vAC = (xc - xa ; yc - ya)
Si xb-xa * yc-ya - xc-xa * yb-ya = 0
alors
ecrire "points alignés"
sinon
ecrire "points pas alignés"
Sortie : Fin de Si
J'ai vraiment du mal à comprendre ; même si je connais la formule pour la mettre sous forme d'un algorithme c'est plus dur ! Je suis désolée si je donne l'impression de ne rien comprendre ...
Pauuline a écrit:En clair le traitement c'est :
vAB = (xb - xa ; yb - ya)
vAC = (xc - xa ; yc - ya)
Si xb-xa * yc-ya - xc-xa * yb-ya = 0
alors
ecrire "points alignés"
sinon
ecrire "points pas alignés"
Sortie : Fin de Si
J'ai vraiment du mal à comprendre ; même si je connais la formule pour la mettre sous forme d'un algorithme c'est plus dur ! Je suis désolée si je donne l'impression de ne rien comprendre ...
Bah un algorithme c'est juste la description d'un calcul...
Un algorithme c'est juste la réponse à "comment faire pour...".
Du genre "je mets tout à gauche, je factorise et je fais un tableau de signes" c'est un algorithme pour résoudre une inéquation.
Bon sinon tu y es presque ; il manque juste quelques parenthèses :
Si (xb-xa) * (yc-ya) - (xc-xa) * (yb-ya) = 0
gigamesh a écrit:Bah un algorithme c'est juste la description d'un calcul...
Un algorithme c'est juste la réponse à "comment faire pour...".
Du genre "je mets tout à gauche, je factorise et je fais un tableau de signes" c'est un algorithme pour résoudre une inéquation.
Bon sinon tu y es presque ; il manque juste quelques parenthèses :
Si (xb-xa) * (yc-ya) - (xc-xa) * (yb-ya) = 0
Oui ça paraît simple mais le mettre sous forme mathématiques c'est moins simple.
Donc si je rajoute les parenthèses à ce que j'ai écrit précédemment, c'est bon ?
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
