Changement de variable

[Ben314]

Oui, dans le cas de cette intégrale :
, où on prendre , la fonction f est effectivement définie sur .
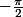
Par contre les bornes d'intégration de départ et deviennent évidement et , c'est à dire qu'elles ne couvrent pas tout l'ensemble de définition de f.


@Euler911 : A noter tout de même que dans ton théorème il semble que l'on ait besoin de l'injectivité de alors que dans le cas "bébète" où on a des primitives, on n'a besoin d'absolument aucune hypothèse sur ... C'est quand même un peu bizare : je me demande si, dans le cas de la non injectivité de , le problème n'est pas que l'intégrabilité de f sur ne donne évidement pas le début de la moitié d'une information concernant la fonction sur la partie de [a,b] telle que soit en dehors de .
Donc, pour que le résultat (avec non injective) soit valable, il faut absolument avoir dans les hypothèse un truc qui dise que est intégrable sur [a,b].
Dans le cas "primitives", c'est les hypothèse de continuité de tout le monde qui le dit.

[Euler911]

Hm, je ne sais pas ce qu'on peut ajouter sans l'injectiviter du cgmt de variable... Mais c'est le thm le plus général que j'ai trouvé... Pour le reste, oui, il faudrait sans doute avoir une hyp sur l'intégrabilité de (fog)g'... mais c'est tortueux:p (Et en regardant le thm que j'ai énoncé, il me semble qu'il englobe toutes les fonctions L-intégrable.)

Bref... c'est compliqué tout ça!