Exercice d'analyse numérique

[yourgod2000]

Bonjour, voici l'énoncé:
On considère la fonction f(x) = x^3+4x-10.
L'étudier, déterminer le nombre de ses racines et appliquer la méthode de Newton pour les calculer.
Je sais tout faire jusqu'au moment où je fais g(x) = x - (f(x)/f'(x)) et que je dois ensuite calculer g'(x) et g''(x). g(x) est une fraction de polynômes donc la dérivée et la dérivée de dérivée vont forcément me donner un résultat compliqué.
Y a t-il une technique particulière à appliquer dans ce cas pour appliquer la méthode de Newton?(trouver la constante de g contractante et trouver si l'intervalle I est stable par g)
Merci d'avance.

[Finrod]

Essai de lire Wikipédia déjà : [url]http://fr.wikipedia.org/wiki/Méthode_de_Newton[/url]

[gigamesh]

Bonjour,
on a
donc si
* f est C²
* avec non nul
alors et par continuité |g'|<1 au voisinage de

[Ben314]

Salut,
La façon dont je comprend l'énoncé (plus précisément le "appliquer la méthode de Newton") signifie que l'on ne te demande absolument de refaire la preuve de la méthode, mais plutôt de donner un (ou des) exemples de U0 qui donneront une suite qui tend vers tel ou tel racine de f.

Comme tu as étudié f, tu doit avoir un tableau donnant le signe de f", celui de f' et un encadrement (même vague) des différentes solutions de f(x)=0.

Pour pouvoir appliquer à coup sûr la méthode de newton et trouver avec une trés grande précision la valeur d'une des solutions x0 de f(x)=0, il faut se placer sur un intervalle [a,b] contenant x0 et sur leque f" ne change pas de signe.
Ensuite, il faut prendre U0=a ou bien U0=b selon le signe de f" sur l'intervalle et selon le signe de f'(x0) (i.e. selon le sens dans lequel la courbe coupe l'axe des x)
Il y a donc 4 cas et, perso, je fait un mini dessin pour retrouver dans chacun des cas si on doit prendre U0=a ou U0=b.
Par exemple, si f">0 et f'(x0)>0, il faut prendre U0=b.
Essaye de faire un dessin correspondant aux 3 autres cas et de voir dans chacun d'eux de quel coté il faut partir...

En résumé, pour moi, la réponse à la question consiste à dire :
Pour telle racine, je me place sur l'intervalle [?,?] sur lequel f" est ? (>0 ou <0) et je prend U0=?. Aprés ? itérations à la calculatrice, j'obtient comme approximation ?,????????

[gigamesh]

Salut,
"il faut" se placer sur un intervalle où f'' ne s'annule pas.

Non. Il suffit.

CEX et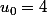

on a la suite 4 2.5 -11 -6.68... -3.835.... -1.987.... etc et ça converge bien.

Bon d'accord c'était juste histoire d'être chiant :bad: , il n' y a que les deux premiers termes qui sont dans f''>0

Quand même : l'unique solution est dans ]-oo;2[.
Par construction (u_n) décroît tant qu'on reste dans f>0; à supposer qu'elle reste au dessus de 2, elle convergerait vers une limite >=2 ce qui est absurde.
Donc à un moment où à un autre on va arriver dans f''<0

Bon il faut juste éviter les u_0 qui nous amèneraient à u_k=2 car f'(2)=0.

Un meilleur contre exemple serait

Bon je sors.

[Ben314]

Là, je trouve que tu charrie un peu : il me semble que, lorsqu'un théorème dit "A=>B", tu à le droit d'utiliser le mot "il faut" dans un phrase du type "pour pouvoir appliquer le théorème il faut que A soit vrai" et il me semble que c'est bien ce qu'il fallait comprendre dans mon post : la méthode de newton est garantie contre toute malfaçon lorsque f" ne change pas de signe (le A du "théorème" est donc bien "f" ne change pas de signe)
Bon, ensuite, effectivement, le théorème n'est pas une équivalence, donc on peut trés bien avoir B (i.e. la convergence vers une racine de f) sans avoir A.

[gigamesh]

Bonsoir Ben,
oui, je charrie.
Mais bon c'était pour le plaisir de chercher un contre exemple.

En tout cas je suis évidemment d'accord avec le fait qu'on utilise souvent "il faut" dans le sens "voila les conditions dont on a besoin pour pouvoir appliquer tel théorème".
Je n'irai pas jusqu'à dire que c'est une pratique souhaitable (sauf si on précise bien "il faut gnin gnin pour appliquer le théorème truc", ce qu'on fait rarement).

Tiens un exemple pour quatrièmes (mais ça marche aussi avec des secondes).
Calculer les angles du triangle 7 7 10.

Si tu dis "pour appliquer cos il nous faut un triangle rectangle" tu bloques un peu les élèves ; puisqu'il n'y en a pas, on est bien embêté.

Si tu dis "pour appliquer cos il suffit d'un triangle rectangle", peut-être que ça incite un peu plus à tracer une hauteur bien choisie ?

Bon j'arrête vu que je n'arrive qu'à peine à me convaincre moi-même. En fait dire "il faudrait" ou il "suffirait" devrait suffire. Il faut un conditionnel quoi. :happy2: