Démontrer un alignement
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Mai 2010, 22:03
par Dinozzo13 » 29 Mai 2010, 22:03
Salut à vous, j'ai un petit soucis, je n'arrive pas à résoudre un petit exercice de géométrie vectoriel, merci d'avance pour votre aide.
Soit ABC un triangle. On définit respectivement les points M et N par
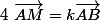
et
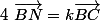
où

.
On nomme les points I,J et G tels que I est le milieu de [AB], J celui de [BC] et G celui de [MN].
Démontrer que les points I, J et G sont alignés.
J'ai pensé à exprimer

et

pour avoir

mais cela ne me mène à rien.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Mai 2010, 22:24
par Ericovitchi » 29 Mai 2010, 22:24
il faut exprimer les coordonnées de tous les points dans le repère AB,AC
I(1/2,0) ; J(1/2,1/2) ; Tu trouves AG avec AG=(AM+AN)/2= ...
Et après tu montreras qu'ils sont alignés en montrant que le coordonnées des vecteurs IJ et IG sont proportionnelles.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Mai 2010, 22:27
par Dinozzo13 » 29 Mai 2010, 22:27
Ok.
Et par curiosité, comment faire sans passer par les coordonnées ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Mai 2010, 00:54
par Ben314 » 30 Mai 2010, 00:54
Tu peut traduire "mot à mot" la méthode avec coordonnées en traduisant par exemple J:(1/2,1/2) par sa définition, c'est à dire
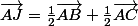
ça permet de prétendre que tu n'utilise pas les coordonnées.
En résumé, tu cherche seulement à écrire tout ce qui est dans l'énoncé en fonction de deux vecteurs fixés, par exemple

et

.
Evidement, ce n'est absolument pas une méthode "différente", seulement une façon différente de rédiger...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Mai 2010, 00:56
par Dinozzo13 » 30 Mai 2010, 00:56
Ok, donc il n'existerai pas d'autre oyen que de passer par les coordonnées ou de faire du "mot à mot" ?
-
friandise
- Membre Naturel
- Messages: 15
- Enregistré le: 26 Mai 2010, 18:58
-
 par friandise » 30 Mai 2010, 01:00
par friandise » 30 Mai 2010, 01:00
Si, il faut essayer d'exprimer
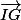
en fonction de
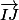
.
Transforme l'écriture de
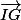
jusqu'à ce que tu tombes sur

-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 30 Mai 2010, 07:19
par beagle » 30 Mai 2010, 07:19
on n'a pas le droit à Thalès lorsqu'on utilise les vecteurs?
Ou faire du Thalès sans le dire?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
friandise
- Membre Naturel
- Messages: 15
- Enregistré le: 26 Mai 2010, 18:58
-
 par friandise » 30 Mai 2010, 08:27
par friandise » 30 Mai 2010, 08:27
beagle a écrit:on n'a pas le droit à Thalès lorsqu'on utilise les vecteurs?
Ou faire du Thalès sans le dire?
Le théorème de Thalès vectoriel :
Soit ABC un triangle quelconque et les points M et N tels que,
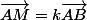
et
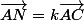
, nous avons alors
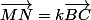
.
Mais où veux-tu donc l'utiliser ?
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 30 Mai 2010, 08:53
par beagle » 30 Mai 2010, 08:53
en utilisant M' tel que BM'=kBA,
utiliser les triangles ABC et MM'N,
en mettant des vecteurs là-dedans mais en faisant du thalès ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Mai 2010, 09:12
par benekire2 » 30 Mai 2010, 09:12
J'ai l'impression qu'on tourne autour du pot, je crois que toutes les méthodes sont les mêmes, coordonnées, simulation de coordonnées ou Thalès, qui se démontre grâce à la relation de Chasles.
Maintenant je propose une solution plus longue qu'avec les coordonnées, que Dinozzo cherchait peut être : ( elle ne se veut pas différente bien sûr)
Tout est en vecteur.
IJ=1/2 (AB+BC)
IG=IM+MG=IA+kAB+MA+AB+BN+NG
soit après réduction IG=1/2 AB +kBC+NG
or NG=-1/2 BN+1/2 BA +1/2 AM = (k-1)/2 AB-k/2BC
d'où en remplacant :
IG=1/2 AB +kBC+NG=IG=1/2 AB +kBC+(k-1)/2 AB-k/2BC =(k/2)AB+(k/2)BC=kIJ
donc IG=kIJ
les points I,G et J sont alignés.
-
friandise
- Membre Naturel
- Messages: 15
- Enregistré le: 26 Mai 2010, 18:58
-
 par friandise » 30 Mai 2010, 09:29
par friandise » 30 Mai 2010, 09:29
Merci d'enlever la réponse, nous ne sommes pas là pour résoudre les exercices des autres, mais de les aider à les résoudre eux-même.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Mai 2010, 10:37
par Ben314 » 30 Mai 2010, 10:37
Si tu veut une "explication" concernant la "méthode benekire", c'est la même idée qu'avec les coordonnées : au départ on a A, B ,C et tout les autres points sont construits à partir de ces 3 là, donc on doit pouvoir tout exprimer en fonction des 3.
L'objectif étant de montrer que I, J et G sont alignée en utilisant le calcul vectoriel, on peut par exemple exprimer les vecteurs IJ et IG en fonction de A,B et C pour voir s'ils sont colinéaires.
1) Pour le vecteur IJ : il faut éliminer I et J à l'aide de leur définition donc faire apparaitre AI=1/2.AB ou BI=1/2.BA ainsi que BJ=1/2.BC ou CJ=1/2.CB.
Pour faire les deux en même temps, il suffit d'introduire le point B :
IJ=IB+BC=1/2.AB+1/2.BC=1/2(AB+BC)=1/2.AC
[en fait on vient de (re) démontrer le théorème des millieux]
2) Pour IG : il faut éliminer I et G à l'aide de leur définition comme çi dessus.
Cela conduit (par exemple) à écrire
IG=IA+AM+MG=1/2.BA+AM+1/2.MN
Maintenant, il faut éliminer M et N en utilisant leurs définition, c'est à dire en faisant apparaitre AM=k.AB et BN=k.BC :
IG=1/2.BA+AM+1/2.(MA+AB+BN)=1/2.BA+k.AB+1/2.(k.BA+AB+k.BC)
Ensuite, on simplifie en regroupant les termes "identiques" :
IG=(-1/2+k-k/2+1/2)AB+k/2.BC=k/2.AB+k/2.BC=k.2.(AB+BC)=k/2.AC
Conclusion : il apparait clairement que IG=k.IJ
Je le (re)dit : cette méthode est identique à celle consistant à utiliser un repère, seule la présentation est différente.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Mai 2010, 10:49
par benekire2 » 30 Mai 2010, 10:49
friandise a écrit:Merci d'enlever la réponse, nous ne sommes pas là pour résoudre les exercices des autres, mais de les aider à les résoudre eux-même.
salut friandise, connaissant dinozzo je t'assure qu'il ne mandie pas les réponses, l'exercice il a du le réussir avec 3 méthodes proposées, j'en propose une autre c'est tout. Je ne lui ai pas fait l'exo. Cordialement.
Ben: Bien sûr la méthode reste la même ... et je ne prétend pas qu'elle soit différente, juste écrit en plus long et plus "vectoriel". Mais de toute façon les coordonées c'est juste du vectoriel dans une base après tout .
-
friandise
- Membre Naturel
- Messages: 15
- Enregistré le: 26 Mai 2010, 18:58
-
 par friandise » 30 Mai 2010, 13:39
par friandise » 30 Mai 2010, 13:39
Ok, bon ben je mets ce que j'avais évoqué avant, solution purement vectorielle.
Je mets toutes les étapes pour ne pas se perdre...
Nous avons :

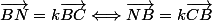
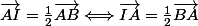
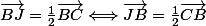
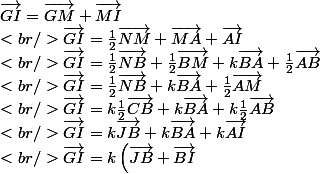 \\<br /><br />\vec{GI} = k\vec{JI} \\)
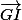
et
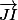
colinéaires et ont un point en commun, d'où G, I et J alignés. CQFD
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 30 Mai 2010, 14:46
par beagle » 30 Mai 2010, 14:46
longtemps que je n'ai pas touché à un vecteur,
donc il me semble comprendre la démarche "purement" vectorielle,
qui pourrait me semble-t-il ètre une démarche algébrique,
donc de "cuisine"-"technique" avec ses forces, comme celles de manipuler des choses limites incompréhensibles, sans ètre limité par une représentation.
Mais comme Dinozzo qui n'est pas un manche, semblait en "difficulté",
je me suis dit que partir de la représentation géométrique, pour en tirer un déroulement algébrique reposant sur une logique de représentation était peut-ètre une possibilité.
il me semble que l'exo se prète tout à fait bien à Thalès, mais on touche là une limite celle de s'appuyer sur une représentation qui n'est pas nécessaire et qui s'avère certainement à un niveau plus élevé difficile à impossible,...
enfin j'en sais rien en fait.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Mai 2010, 18:20
par benekire2 » 30 Mai 2010, 18:20
je tient a signaler que la méthode de friandise est sensiblement la même que la mienne, et que bien que ce soit réellement une solution vectorielle, comme l'a signalé ben, on a TOUS la même méthode ici, puisque on s'est servi d'une base.
-
friandise
- Membre Naturel
- Messages: 15
- Enregistré le: 26 Mai 2010, 18:58
-
 par friandise » 30 Mai 2010, 20:21
par friandise » 30 Mai 2010, 20:21
benekire2 a écrit:je tient a signaler que la méthode de friandise est sensiblement la même que la mienne, et que bien que ce soit réellement une solution vectorielle, comme l'a signalé ben, on a TOUS la même méthode ici, puisque on s'est servi d'une base.
En effet, on va dire que j'y ai mis une meilleure présentation

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Mai 2010, 20:32
par benekire2 » 30 Mai 2010, 20:32
friandise a écrit:En effet, on va dire que j'y ai mis une meilleure présentation

Oui :we: C'est que mettre des vecteurs ça m'aurait pris ... beaucoup de temps a vrai dire ..
-
JoeD.
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Juin 2010, 14:36
-
 par JoeD. » 01 Juin 2010, 14:56
par JoeD. » 01 Juin 2010, 14:56
Vous vous embêtez pour pas grand chose.
Il y a beaucoup plus simple et élégant : déterminez une homothétie qui lie les trois points concernés. En trouver une respectant cette condition répond à la question par définition.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Juin 2010, 08:11
par Ben314 » 02 Juin 2010, 08:11
Pour donner mon opinion concernant toutes les "méthodes" sus mentionnées, il faut quand même dire qu'il y a deux "fils conducteurs" légèrement différents :
1) On essaye de faire de la "jolie géométrie" en faisant un dessin et en essayant de comprendre "comment ça marche" : c'est grosso modo ce que proposent beagle et JoeD. C'est en général bien plus court, et bien plus joli, mais... cela demande de l'imagination.
2) On fait aucun dessin, et on utilise les coordonnées ou tout autre méthode plus ou moins "systématique" consistant à tout écrire en fonction de trés peu de point : c'est ce que propose Ericovitchi et moi (benekire et friandise étant un peu intermédiaires mais plutôt de ce coté là). C'est en général trés bourrin, plus long et considéré comme nettement mois joli mais... c'est parfaitement mécanique et donc ne demande aucune imagination.
A mon sens (donc ça se discute), la géométrie "analytique" (i.e. avec des vecteurs et/ou des coordonnées) à un peu été inventé pour ce coté "mécanique" et pas super subtil ce qui fait que, quand on demande une preuve par l'analytique, pour moi, ça veut un peu dire "à la bourrin" et sans même faire de dessin.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités