Changement de variable

[AceVentura]

Bonsoir,

est-il vrai que pour utiliser la formule du changement de variables , n'as pas besoin d'être bijective ? J'ai un petit doute ! Quel est l'énoncé exact ? Merci d'avance.

[Ben314]

Ca dépend un peu du contexte, mais dans le cas de fonctions continues sur un intervalle fermé borné (i.e. ou on peut parler des primitives en question), la "formule de changement de variable" n'est jamais qu'une façon légèrement différente d'exprimer la "régle de dérivation" et tu doit savoir que, dans cette règle, il n'est nul besoin que soit bijective.

Edit : je viens de voir que tu t'est gourré dans la fameuse formule.
C'est
où F est une primitive de f (qui doit être définie et continue sur qui n'est pas forcément lorsque n'est pas bijective)

[AceVentura]

Oui, j'ai inversé ! Par contre, j'ai toujours du mal sur les conditions. f est une fonction de [a,b] (avec a<b) dans 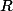, continue. Et ? Si l'on veut pouvoir composer, il faut que (avec I intervalle de définition de la fonction , non ?
Après, est au moins dérivable, mais je ne sais pas s'il faut supposer la continuité de sa dérivée (ie de classe C^1)

[Ben314]

Pour pouvoir écrire ça : , il faut que f soit définie et intégrable sur (ou sur )
Pour pouvoir écrire ça : il faut que soit définie sur [a,b] (ou [b,a]) et que f soit définie sur ce qui, si n'est pas bijective, est plus fort que de demander seulement que f soit définie sur

Si est uniquement dérivable et que sa dérivée n'est pas continue, il n'est pas du tout évident que la fonction soit intégrable sur [a,b].

[AceVentura]

Oui, mais ... je dois avouer que tu m'as bien embrouillé la, même si tout ce que tu dis me semble plus que correct !
Finalement, que dois-je dire ? Soit avec . Si f ..... et ..... alors :hein: :hein:

[Euler911]

Bonjour,

Voici un théorème de changement de variable:

Soient tels que et , et . Si est intégrable et si est monotone et dérivable sur , alors la fonction est intégrable sur et

[Ben314]

Enoncé 1 (largement suffisant pour la plupart des calculs type Lycée) :

Si est une fonction de classe C1 bijective de I=[a,b] (ou I=[b,a]) sur
(donc ou selon la monotonie de et le fait que a<b ou pas)
et f est une fonction continue de J dans alors :

Qui, si on pose et peut s'écrire :

qui permet d'avoir tout les du même coté de l'égalité.

Enoncé 2 (Plus général, exactement la même preuve que l'énoncé 1, mais pas franchement utile pour la plupart des calculs type Lycée) :

Si est une fonction de classe C1 de I=[a,b] (ou [b,a]) dans et f est une fonction continue de dans alors :

Remarques :
- Ici, il n'y a aucune raison que ou )
- Comme n'est pas bijective, il n'y a pas de "deuxième écriture" utilisant

[Ben314]

Bonjour,

Voici un théorème de changement de variable:

Soient tels que et , et . Si est intégrable et si est monotone et dérivable sur , alors la fonction est intégrable sur et

Dans cette version là (notations "ensemblistes" des intégrales qui interdit les "intégrales dans le mauvais sens"), il y a un problème dans la notation dans le cas où est décroisssante.
Il faut :
- Soit supposer croissante.
- Soit ne rien supposer du tout et, dans ce cas, remplacer par et rajouter une valeur absolue autour du dans l'intégale.

[Euler911]

mh... oui, je n'avais pas fait attention à ça, désolé...
Correction:

ça doit fonctionner comme ça;)

[AceVentura]

Ok Ben pour l'énoncé 2. Peux-tu me faire la preuve, on écrivant tout de manière très précis ? J'ai l'impression d'en oublier ! On part de la règle de dérivation . L'idée maintenant, c'est d'intégrer cette égalité et il faut pouvoir le faire !
Je m'aperçois à l'instant que j'ai écris de manière naturelle f' dans le second membre de l'égalité : est-ce une erreur de ma part ?

[Ben314]

Ben, la preuve, elle est à la fin de mon post #2...

[AceVentura]

Ok ! Si est bijective, alors ?

As-tu un exemple de calcul avec la bijectivité et la non bijectivité ?
Par exemple ?

[Ben314]

Ok ! Si est bijective, alors ?

As-tu un exemple de calcul avec la bijectivité et la non bijectivité ?
Par exemple ?

Pour ta première question, on a si est croissante. Si elle est décroissante, on a .

Pour des exemples de changement de variables bijectif ou pas, le premier truc qui me vient à l'esprit, c'est avec de la trigo :
Pour , on peut prendre qui est bijectif.
Pour , on peut prendre qui n'est pas bijectif.

[AceVentura]

Dans le cas non bijectif, j'écris donc :


avec et .

J'ai un léger doute sur l'ensemble de définition de la fonction f.

[Nightmare]

Une autre preuve de la formule de changement de variable, avec hypothèse supplémentaire de monotonie (Cf post d'Euler) dont j'avais déjà parlé sur le forum il me semble :

On subdivise le segment en . Les bases des rectangles ont pour longueur, d'après le TAF, avec un certain .

La somme de Riemann converge vers mais vaut aussi qui converge vers ... :lol3:

:happy3:

[Euler911]

Je me demande si l'énoncé de thm 2 de Ben peux se passer de la continuité de f...

[Ben314]

Je me demande si l'énoncé de thm 2 de Ben peux se passer de la continuité de f...

Trés honètement, j'en sais rien...
Je sais que le résultat est trivial dans le cas où tout est bien sage (i.e. qu'en fait c'est du calcul de primitive).
Evidement, ça se généralise immédiatement à tout ce qui est "bien sage" par morceaux.
D'un autre coté, si tu suppose seulement dérivable mais pas forcément C^1 ni monotone, je pense pas que tu ait forcément l'intégrabilité de , mais c'était pas ça ta question (en plus, il faut s'entendre sur le sens de "intégrable" : Riemann ? Lebesgue ? Autre ?)

A mon avis, si f est intégrable (Riemann) et C^1 (mais pas forcément monotone), ça doit marcher, mais j'ai la flemme de chercher...

[Euler911]

hm, j'utilise l'intégrale de Kurzweil-Henstock pour ma part qd on utilise une fct de [a,b]->R... j'ai aussi l'impression que ça reste correct si on modifie la fonction sur un ensemble négligeable mais sinon... aucune idée... j'y réfléchirai un de ces 4...

[Euler911]

Je pense avoir la réponse:

Si on intègre au sens de mcshane ( ou au sens de lebesgue, c'est équivalent)

On a le thm suivant, plus général:

Soient un ouvert borné de frontière négligeable, une fonction telle que soit injective et . Si à un jacobien sur U, alors f est intégrable sur si et seulement si la fonction est intégrable sur . Etc.

ça s'adapte à notre cas il me semble.

Je n'ai pas la démo pr l'instant par contre... mais je pense qu'elle doit être asser technique...:s

EDIT: on a juste l'injectivité en plus:p

[AceVentura]

Merci les amis pour ces contributions ! Cependant, je tient à rappeler que le niveau est largement inférieur. L'énoncé de Ben me convenait, j'espère qu'il reste toujours "valable".
Donc l'exemple qu'il a traité, fait dans le cas non bijectif, je trouve bien ln(2). J'ai juste un petit doute sur l'espace de définition de la fonction f. Est-ce bien ?