Géometrie dans l' espace

[mimilamouse]

Soient A(1 ; 2 ; 0), B(2 ; 2 ; 0), C(1 ; 3 ; 0) et D(1 ; 2 ; 1) quatre points de l’espace muni
d’un repère orthonormal (O,i,j,k)

(P) désigne le plan orthogonal à (BC) contenant A ;
(Q) désigne le plan orthogonal à (DC) contenant A ;
(R) désigne le plan orthogonal à (BD) contenant A.

1. Montrer que le plan (P) a pour équation cartésienne x - y + 1 =0
On admet que le plan (Q) a pour équation cartésienne - y +z + 2=0 et que le
plan (R) a pour équation cartésienne -x +z + 1=0

2. a. Résoudre le système :

x-y+1=0
-y+z+2=0
-x+z+1=0

b. En déduire que l’intersection des trois plans (P), (Q) et (R) est une droite
(d) passant par le point E(2 ; 3 ; 1).
c. Vérifier que la droite (d) est orthogonale au plan (BCD).
En déduire une équation cartésienne du plan (BCD).

3. Déterminer une équation cartésienne pour chacun des plans (ABC), (ABD) et
(ACD).

4. a. Montrer que tout point M de la droite (d) est équidistant des plans
(ABC), (ABD) et (ACD).
b. Existe-t-il des points de l’espace équidistants des plans (ABC), (ABD),
(ACD) et (BCD) ?

[Ericovitchi]

rappelles toi qu'un plan qui a pour équation ax+by+cz+d=0 a pour vecteur normal (a,b,c)
donc par exemple, pour trouver "le plan orthogonal à (BC) contenant A"
tu calcules les coordonnées de BC, tu sais qu'elles sont proportionnelles à a,b,c. Tu dis qu'il passe par A pour trouver l'équation.

[mimilamouse]

POur la question 2)c

le vecteur directeur c'est la droite d ?
En tout cas ses coordonnées sont (-1,-1,1)

et cellles de BC (-1,1,0)

On fait le produit scalire de BC.d=xx'+yy'+zz'

On doit trouver 0 pour dire que c'est orthogonal

[Ericovitchi]

Déjà tu as montré que la droite (d) était l'intersection des 3 plans. Chacun de ces plans sont respectivement orthogonaux BC,BD et CD donc la droite l'est aussi et elle est donc orthogonale à BCD.

Pour trouver l'équation de BCD. il te suffit d'avoir un vecteur de la droite (d)
poses par exemple x=t tu en déduis y=t+1 et z=t-1 tu as des coordonnées paramétriques de (d) et donc un vecteur directeur (1,1,1)

le plan BCD a donc une équation genre x+y+z+h=0 pour trouver h il suffit de dire que B est dans le plan h=-4
le plan est donc x+y+z=4 (vérifies que C et D sont bien dedans )

[mimilamouse]

Il faut faire pareil pour la question 3 ?

[Ericovitchi]

je ne sais pas trop ce que tu appelles "pareil", tu n'as pas exactement les mêmes éléments que pour la question d'avant.
Mais essayes de construire un raisonnement, nous corrigerons si besoin.

[mimilamouse]

Pzar exemple pour leplan ABC il faut que je me sere des coordones des vecteurs AB et BC ?

[Ericovitchi]

Effectivement, c'est une façon de trouver l'équation d'un plan ; en passant par les équations paramétriques du plan.
Si tu connais un point A du plan et 2 vecteurs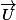 et 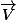tu peux dire que tout point M du plan est tel que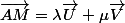
Tu écris ça pour chaque coordonnées des vecteurs. Ca te fait 3 équations. Et si tu élimines et entre ces 3 équations, tu trouves l'équation du plan