Racines d'un polynôme

par **merayone** » 22 Mai 2010, 16:08

Bonjour !

Existe-t-il une formule permettant de calculer le produit des racines d'un polynôme ? Est-ce que le produit de ces racines est = (coef constant) / (coef dominant) pour un polynôme de degré n N où n'est-ce vrai que pour les trinômes du second degré ?

par **Nightmare** » 22 Mai 2010, 16:10

Salut,

C'est vrai pour n'importe quel polynôme et dû à la factorisation

par **Finrod** » 22 Mai 2010, 16:11

SI tu développes

tu obtient que le coefficient constant est égal à

.

Donc la formule pour les polynome du second degres se généralise en ajoutant le

, qui vaut 1 pour n=2.

par **Ericovitchi** » 22 Mai 2010, 16:12

Essayes de trouver toi-même.

Si tu développes an(x-x1)(x-x2) .... (x-xn) et que tu dis que c'est égal à

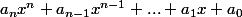
Combien va valoir le produit des racines ?

Edit : grillé et par 2 à la fois. Vous êtes rapides aujourd'hui, on voit qu'il n'y a pas beaucoup de posts !

par **merayone** » 22 Mai 2010, 16:16

Wow que de réponses ! :D

Justement Ericovitchi, je n'arrive pas à raisonner pour passer du produit des (X-xi) au produit des xi. Et je ne comprend pas trop le raisonnement de Finrod, je dois avoir manqué quelque chose mais je ne vois pas quoi !

par **Finrod** » 22 Mai 2010, 16:19

Fait des cas particuliers de degrés 3 ou 4, ça devrait t'apparaitre clairement.

par **merayone** » 22 Mai 2010, 16:30

J'obtiens l'opposé du produit des racines comme terme constant, je pense que j'ai une belle erreur de factorisation !!!

par **merayone** » 22 Mai 2010, 16:47

Est-ce que quelqu'un peut me montrer la démo svp ?
Non pas que j'en ai besoin pour mon exercice (admettre le résultat me suffit) mais j'aimerais quand même le comprendre ! :triste:

par **Ericovitchi** » 22 Mai 2010, 18:04

Regardes ce qui donne le terme constant des deux cotés de l'équation.
Coté produit le seul terme constant c'est le produit de tous les -xi entre eux (avec an devant) et comme il y en a n ça donne an.(-1)^n x1.x2. ... xn
et de l'autre le terme constant c'est a0
et donc le produit des racines vaut donc

par **merayone** » 22 Mai 2010, 18:16

Pourquoi "avec an devant" ?

par **Ericovitchi** » 22 Mai 2010, 18:35

il faut bien que les deux termes en x^n soient également égaux donc
pour que le produit de tous les x fasse anx^n il faut bien que le produit soit
an(x-x0)(x-x1) ...

par **Finrod** » 23 Mai 2010, 07:22

merayone a écrit:J'obtiens l'opposé du produit des racines comme terme constant, je pense que j'ai une belle erreur de factorisation !!!

Si tu as trouvé ça pour n=3, c'est normal. Je te rappelle que

.
et tu as visiblement oublié de parler du coeff dominant qui se retrouve aussi en facteur (tu l'as peut être pris égal à 1 sans faire exprès).

par **merayone** » 23 Mai 2010, 14:35

UUUUUP SVP ! :happy2:

Racines d'un polynôme

Racines d'un polynôme

Qui est en ligne