Suite harmonique

[AceVentura]

Bonjour,

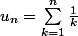
je me demande s'il est possible avec la seule définition du fait qu'une suite diverge (cas général ou cas ) que la suite diverge (... vers !).

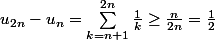
Je montrer que est ce suffisant ?

[Nightmare]

Salut,

oui, car R est complet !

Edit : Sans invoquer le fait que la suite ne soit pas de Cauchy, si u(n) convergeait, u(2n) convergerait vers la même limite et donc u(2n)-u(n) vers 0...

[AceVentura]

En fait, on suppose donné cet exercice avant d'avoir traiter les opérations sur les limites. Est-il possible de le faire "à coup de epsilon" ?

[Doraki]

Il est toujours possible de montrer un truc en utilisant la définition.
Donc oui tu peux montrer que la suite n'est pas convergente :

Soit l dans R quelconque, prends epsilon < 1/4, et montre que la suite un ne peut pas être confinée à [l-epsilon ; l+epsilon] à partir d'un certain rang, ce qui empêche un de converger vers l.

Mais là le truc à montrer c'est plutôt que la limite tend vers + l'infini.

[AceVentura]

En fait, je voudrai exactement :

qui est la définition de la divergence.

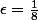
Avec par exemple, il faut donc prouver que . Je m'aperçois que je ne sais pas traduire ceci en ... sous la forme d'un intervalle !

[Doraki]

Ben tu peux toujours faire un dessin pour mieux voir.
En tout cas pour voir que ce n'est pas un intervalle.

Si tu veux rester formel tu peux toujours faire deux cas selon le signe du truc à l'intérieur de la valeur absolue.

Mais là, si tu as conscience du fait que un augmente, tu trouveras plus facilement un n tel que (un - l) soit positif, comme ça tu peux retirer la valeur absolue.

Et enfin, je pense que entre n = N ou n = 2N, y'a forcément l'un des deux qui vérifie |un - l|>= 1/8.

[Ben314]

Sinon, en restant à un niveau trés élémentaire, une minuscule récurrence te montre que l'inégalité implique que et, comme ta suite est croissante, cela implique qu'elle tend vers l'infini. (immédiat avec la déf. d'une suite qui tend vers +oo)

[AceVentura]

Salut Ben,
en fait, avec "ta" méthode, on utilise déjà une minuscule proposition de comparaison des limites : si à partir d'un certain rang et que diverge vers , alors aussi (que l'on peut même compléter en disant que si diverge vers , alors aussi).
Est-il possible de faire sans, ie juste par majoration/minoration, usant de la définition et des règles usuelles sur les inégalités ?

[Ben314]

...on utilise déjà une minuscule proposition de comparaison des limites : si à partir d'un certain rang et que diverge vers , alors aussi...

Non :
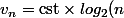Tu n'as absolument pas besoin d'utiliser ce résultat et c'est même trés con de l'utiliser car cela demande de connaitre les fonctions logarithmes et leurs limites (car la seule possibilité raisonable pour la suite qui minore est de la forme où est le log en base 2).

Il est bien plus simple et plus direct d'utiliser (comme je te l'avais dit dans le précédent post...) la définition d'une suite qui tend vers l'infini :

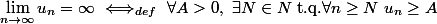
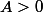
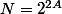
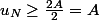
Vu que , partant d'un (supposé entier) quelconque, il suffit de prendre pour avoir puis, du fait de la croissance de la suite,

[AceVentura]

Donc tu viens de montrer que :


Est-ce équivalent à la définition de la limite que j'ai :


?

[chbichib khaled]

il suffit de monter k il ne pas une suite de Cauchy c' ki tu deviens de faire ...

[AceVentura]

Je sais qu'il existe bon nombre de méthode pour montrer cela. Pour ma part, je veux me cantonner à le démontrer en utilisant uniquement la définition de la limite.
C'est ce qu'a fait Ben, et je demande juste l'équivalence entre :

et


Clairement, si c'est vrai qu'il existe etc, alors c'est vrai . Le sens indirect me donne plus de fil à retordre.

[Nightmare]

Salut !

R est archimédien! Soit A réel, E(A)+1 est entier donc minore la suite à partir d'un certain rang, et E(A)+1 > A, donc A aussi.

[Doraki]

Soit A dans R quelconque.
On prend un entier B plus grand que A.
On l'utilise dans l'hypothèse pour obtenir un entier N tel que pour tout n >= N, un >= B
Comme B >= A, on en déduit que pour tout n >= N, un >= B >= A, et donc le même N convient.

[AceVentura]

Ok ! Merci à vous !