Exercice sur les produits scalaires

[pilote S]

Bonsoir tout le monde . Je suis en 1ere scientifique et j ai un devoir maison à faire pour jeudi , le probleme c est que je suis un peu bloquée.
Voici l'enoncé :
Soit un triangle ABC. On pose BC=a , AC=b et AB=c. On sait que l'angle BAC=60° , a=3 et b²+c²=16
Determiner b et c
J'ai essayé de resoudre cet exercice avec les relations d'al-kashi mais je n'y suis pas arrivée .
Si quelqu un pourrait m'expliquer comment commencer cet exercice cela m 'arrangerait beaucoup.
Merci d'avance pour votre aide.

[gigamesh]

Bonsoir,
tu as le système
a=3
b²+c²=16
a²=b²+c²-2bc cos(60) Al Kashi !!! Tu étais tout à fait sur la bonne piste.

si tu te rappelles que cos(60)=1/2, tu vas trouver assez rapidement le produit bc.

ensuite essaie des identités remarquables...

[pilote S]

Bonjour j'ai reussi à calculer bc j ai trouvé bc=7 mais apres pour les identites remarquables je ne vois pas du tout comment faire . Pourriez vous m'expliquer en detail pour trouver b et c. Merci d'avance

[Ericovitchi]

il voulait dire qu'il faut utiliser (b+c)²=b²+c²+2bc ça va te donner b+c et tu seras ramené à trouver 2 nombres connaissant leur somme et leur produit.

[M2aa]

J'ai le même exo, et je trouve pour b+c= 30/7 c'est juste ?

Mais après je vois pas comment faire pour trouver b et c

[Ericovitchi]

non (b+c)²=b²+c²+2bc = 16 + 14= 30 donc

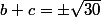
Trouver deux nombres b et c dont on connait la somme S et le produit P, c'est classique, c'est résoudre l'équation du second degré X²-SX+P=0

(que l'on obtient en éliminant une des variable x ou y dans le système x+y=S ; xy=P )