Fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 21:24
par X_lOlly_pOp_X » 17 Mai 2010, 21:24
Bonjour, j'ai la fonction
=\frac{3}{2}e^{2x}-e^{x}-2x-4)
et
=(3e^{x}+2)(e^{x}-1))
On me demande d'en déduire le signe de f'(x), j'ai mis que comme
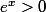
alors c'était positif.
On me demande d'en déduire le tableau de variation de f, j'ai donc mis que c'était toujours croissant sur ]-infini; 1]
Mais après on me demande de justifier que l'équation f(x)=0 admet une solution dans l'intervalle [-3;0]
Et la comment on fait ?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 21:29
par ned aero » 17 Mai 2010, 21:29
salut,
non f' n'est pas positif sur tout lR, e^x>0 ==> 3e^x + 2 >0
donc f' est du signe de (e^x -1)
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 21:32
par X_lOlly_pOp_X » 17 Mai 2010, 21:32
C'est tout ce qu'il faut mettre ??
Qu'il est du signe de
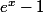
?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 21:42
par ned aero » 17 Mai 2010, 21:42
et chercher le signe de (e^x -1)
e^x -1>0 (donc f'>0) si x....
e^x -1<0 (donc f'<0) si x....
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 21:46
par X_lOlly_pOp_X » 17 Mai 2010, 21:46
e^x -1>0 (donc f'>0) si x appartient a ]-infini;0[
e^x -1<0 (donc f'<0) si x appartient a ]0;1[
Je dis ça mais j'en ai aucune idée en fait lol
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 21:48
par ned aero » 17 Mai 2010, 21:48
faut alors que tu bosses sérieusement tes cours...
par exemple
e^x -1>0 ==> e^x >1 ==> ln e^x >ln1 => x>0 car la fct exp est strictement croissante
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 21:51
par X_lOlly_pOp_X » 17 Mai 2010, 21:51
e^x -1>0 (donc f'>0) si x>ln1
e^x -1<0 (donc f'<0) si x
Nan ?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 21:53
par ned aero » 17 Mai 2010, 21:53
oui
et comme ln1 =0 alors f' >0 si x>0 et f'<0 si x<0
tu peux réaliser le tableau de variation de f
pour l'autre question: voir le théorème des valeurs intermédiaires ou le théorème de la bijection
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 21:56
par X_lOlly_pOp_X » 17 Mai 2010, 21:56
Mais donc dans mon tableau de variation, c'est quand même seulement croissant non ?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 21:59
par ned aero » 17 Mai 2010, 21:59
non
si f '<0 que cela veut il dire?
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 22:04
par X_lOlly_pOp_X » 17 Mai 2010, 22:04
Notre tableau de variation est donc sur -infini ; 1.
Et on met 0 comme Valeur interdite?
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 22:06
par X_lOlly_pOp_X » 17 Mai 2010, 22:06
Mais ça veut dire que c'est impossible non ??!
Vu que on peut pas avec e^x
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 22:11
par ned aero » 17 Mai 2010, 22:11
c'est x qui est négatif pas e^x
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 22:13
par X_lOlly_pOp_X » 17 Mai 2010, 22:13
Ca fait décroissant sur -infini;0 et croissant sur 0;1
C'est ça ?
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 22:17
par ned aero » 17 Mai 2010, 22:17
f(x) est donc décroissante sur ]-oo;0[ et croissante sur ]0;+oo[ et non sur 0;1
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 22:18
par ned aero » 17 Mai 2010, 22:18
je dois partir. A+
-
X_lOlly_pOp_X
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Sep 2008, 14:44
-
 par X_lOlly_pOp_X » 17 Mai 2010, 22:18
par X_lOlly_pOp_X » 17 Mai 2010, 22:18
Mais ma fonction f est définie sur -oo;1 !!!
Bonne soirée, a+
-
ned aero
- Membre Relatif
- Messages: 387
- Enregistré le: 16 Fév 2010, 20:30
-
 par ned aero » 17 Mai 2010, 22:20
par ned aero » 17 Mai 2010, 22:20
Ah OK alors, je ne connaissais pas le domaine d'étude de ta fonction...
je dois partir A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
