Bonjour,
Voici le sujet de mon devoir maison :
[CENTER]

[/CENTER]
Voici ce que j'ai commencé à faire (pour le I) :
1) Conjecture : Les points

sont situés sur une droite perpendiculaire à
)
.
2) Le repère choisi est un repère orthonormal
)
où

est un vecteur directeur de
)
et
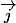
un vecteur directeur de

.
[INDENT]
a. 
est un point de
)
et

est un vecteur directeur de cette droite donc

a une ordonnée nulle. On appelle son abscisse

. Les coordonnées de

sécrivent donc
)
.
De la même façon,

a une ordonnée nulle. On appelle son abscisse

. Les coordonnées de

sécrivent donc
)
.

est un point de

et
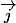
est un vecteur directeur de cette droite donc

a une abscisse nulle. On appelle son ordonnée

. Les coordonnées de

sécrivent donc
)
.[/INDENT]
[INDENT]
b. Déterminons les coordonnées du vecteur normal

à la droite

.

.
)
.
Déterminons léquation de la droite

.
 \in D)
si, et seulement si,
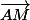
et
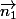
sont orthogonaux
si, et seulement si,

si, et seulement si,
 \times a+y\times(-h)=0)
si, et seulement si,

si, et seulement si,

.
Conclusion : Une équation cartésienne de

est

.
Déterminons les coordonnées du vecteur normal

à la droite
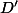
.

.
)
.
Déterminons léquation de la droite
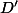
.
 \in D')
si, et seulement si,
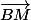
et

sont orthogonaux
si, et seulement si,

si, et seulement si,
 \times b+y\times(-h)=0)
si, et seulement si,

si, et seulement si,

.
Conclusion : Une équation cartésienne de
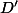
est

.
c. 
est le point dintersection des droites

et
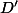
.
Établissons une égalité entre les équations des deux droites afin de trouver les coordonnées de

.

.

.
x-a^2-b^2=0)
.
x-(a-b)(a+b)=0)
.
)
(on simplifie par
)
).
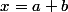
.
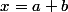
est labscisse du point

. Remplaçons

dans léquation de lune des deux droites afin de trouver lordonnée de

.
-hy-a^2=0)
.

.
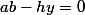
.
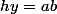
.

.
Conlusion : Les coordonnées du point

sont
)
[/INDENT]
Je bloque à la question
d.
Merci.
 [/CENTER]
[/CENTER]